Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.6 - Ex. 90
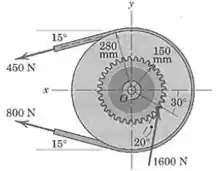
A polia e a correia em presa a ela estão girando no sentido anti-horário e estão submetidas à carga de , devida aos dentes da engrenagem, e aos esforços trativos de e na correia em . Represente a ação destas três forças por uma força resultante em e por um momento de módulo . O conjunto está desacelerando ou acelerando?
Passo 1
Precisamos calcular a força resultante , que é a soma vetorial de todas as forças na figura, então vamos escrevê-las em forma vetorial:
E para a terceira força a projeção é um pouco mais complicada:
E agora podemos calcular a força resultante:
Passo 2
Agora precisamos calcular o momento total dessas forças em relação ao ponto . Começamos fazendo isso para a força de (é importante olhar para a figura para compreender esse cálculo):
Perceba que só essa componente da força produz momento, porque a linha de ação da outra componente passa pelo ponto .
Vamos olhar para as duas forças de tração, como elas estão associadas às polias que dão a volta na engrenagem, podemos achar os momentos de cada uma delas apenas multiplicando seu módulo pelo raio da engrenagem:
Onde o momento da força de acompanha um sinal negativo porque favorece a rotação no sentido horário.
Então o momento total é:
Como temos um torque resultante , podemos garantir que a rotação do sistema é acelerada no sentido anti-horário, já que a velocidade angular inicial também está no mesmo sentido (segundo o enunciado).
Resposta
A força resultante é , o momento é e o conjunto está acelerando no sentido anti-horário.