Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 6.Problemas - Ex. 131

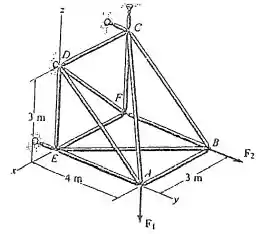
A treliça espacial é sustentada por uma junta esférica em e ligações curtas em e . Determine a força em cada membro e indique se os membros estão sob tração ou compressão. Considere e .

Passo 1

Para determinar as forças, deve-se fazer o diagrama de corpo livre de cada membro no qual sejam indicadas todas as forças atuando no respectivo membro.

Além disso, é possível fazer uma análise prévia das forças aplicadas ao sistema e das reações nos pontos de fixação e determinar algumas informações adicionais. Para tanto, o DCL de todo o sistema é:

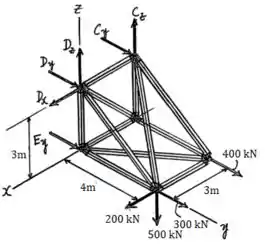
A partir do desenho, é possível descobrir algumas das reações fazendo:

Passo 2

Então, escolhendo a junta primeiro e fazendo o seu DCL, tem-se que:

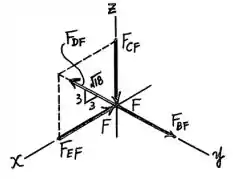
Com isso, é possível determinar as forças atuando nos membros e da treliça através do equilíbrio de forças.

Então,

Como ainda não é possível determinar as outras forças, esta parte será retomada mais à frente.

Passo 3

Para a junta :

Então, fazendo o equilíbrio de forças:

A força está agindo sobre o membro, então, possui caráter trativo. Enquanto isso, a força age sobre a junta e, logo, possui caráter compressivo.

Passo 4

Para a junta :

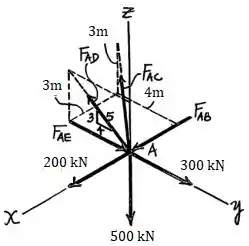
Então, fazendo o equilíbrio de forças:

As forças e agem nos membros da treliça e, por isso, possuem caráter trativo.

A força está agindo sobre o pino, então, possui caráter compressivo.

Passo 5

Em seguida, para a junta :

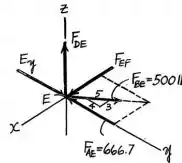
Com o equilíbrio de forças tem-se:

A força age sobre a junta, então, possui caráter compressivo.

Passo 6

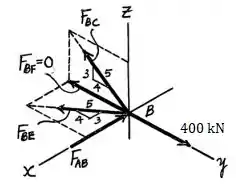
Por fim, para a junta :

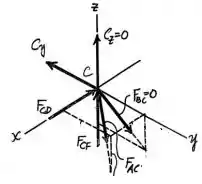
Com o equilíbrio de forças tem-se:

Pode-se, ainda, realizar a análise de forças no eixo para este membro. Fazendo isso:

Tal resultado confere com o valor anteriormente obtido.

Ambas as forças e agem sobre a junta e, portanto, possuem caráter compressivo.

Passo 7

Como dito antes, algumas forças que tinham influência na junta não puderam ser determinadas pois dependiam de , e . No entanto, duas dessas forças foram encontradas possibilitando determinar a outra restante.