Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 11.Problemas - Ex. 18
Na treliça mostrada, todos os elementos são feitos do mesmo material e têm a área da seção trasnversal indicada. Determine a energia de deformação da treliça quando lhe é aplicada a força
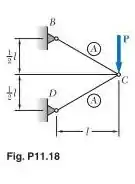
Passo 1
Fala aí, galera. Tudo bem? Bora pra outra questão.
Por trigonometria, sabemos que:
Agora, vamos aplicar as equações de equilíbrio. Aplicando o somatório de força:
Passo 2
A energia de deformação é dada por:
Substituindo os valores das forças, comprimento e os parâmetros do denominador, teremos:
- Prontinho!
Resposta
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Mostrar por integração que a energia de deformação da barra A B , em forma de tronco de cone, é: U = 1 4 P 2 L E A m í n í onde A m í n í é a área de seção transversal na extremidade B .
Usando E = 200G P a , determinar, por meio aproximado, a máxima energia de deformação que pode ser acumulada pela porção A B de 240m m , da barra de controle mostrada, se a tensão normal admissível é
Na treliça mostrada, todos os membros são feitos do mesmo material e têm seções transversais uniformes, com as áreas indicadas. Determinar a energia de deformação da treliça, quando a carga P é aplica
Cada uma das barras de treliça mostrada é feita de alumínio e tem a seção transversal com as áreas indicadas. Usando E = 72G P a , determinar a energia de deformação da treliça para o carregamento mos
Na treliça mostrada, todos os membros são feitos do mesmo material e têm seções transversais uniformes, com as áreas indicadas. Determinar a energia de deformação da treliça, quando a carga P é aplica