Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Estatica das Estruturas por Humberto Lima Soriano- Ed: 3º - Capítulo 1.9 - Ex. 10

Três cilindros de raio r de seção transversal e peso específico ρ estão em repouso nas duas situações esquematizadas na próxima figura. Determine as forças de interação entre esses cilindros e as forças que os anteparos verticais exercem sobre os cilindros

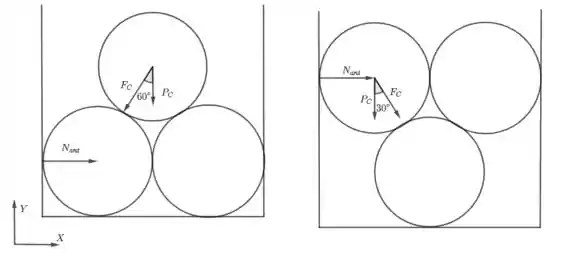
Passo 1

No eixo vertical, temos a força peso do cilindro dada por (Volume do cilindro = π   r 2 l )

P C = ρ V = ρ π r 2 l

A força de interação do cilindro superior nos cilindros inferiores tem componente vertical dada por F C ⋅   c o s   60 ° = 0,5   F C . Assim, o equilíbrio na direção vertical nos dá o módulo da força de interação dos cilindros:

∑ F Y = ρ π r 2 l - 2 ⋅ 0,5 F C = ρ π r 2 l -   F C = 0   ⇒   F C = ρ π r 2 l

Na direção horizontal, temos a normal do anteparo menos a componente horizontal da interação. Assim

∑ F X = N a n t - s e n   60 °   F C = N a n t - 0,866 F C = 0 ⇒ N a n t = 0,866 F C = 0,866   ρ π r 2 l

Passo 2

Na segunda figura, a força de interação de um dos cilindros superiores forma um ângulo de 30 ° com a vertical. Assim,

∑ F Y = ρ π r 2 l - c o s   30 ° F C = ρ π r 2 l - 0,866 F C = 0   ⇒ 0,866 F C = ρ π r 2 l   ⇒ F C = ρ π r 2 l 0,866  

∑ F X = N a n t - s e n   30 °   F C = N a n t - 0,5   F C = 0   ⇒ N a n t = 0,5   F C = 0,5 ρ π r 2 l 0,866 = 0,577 ρ π r 2 l

Resposta

Figura 1:

F C = ρ π r 2 l , N a n t = 0,866   ρ π r 2 l

Figura 2:

F C = ρ π r 2 l 0,866 , N a n t = 0,577 ρ π r 2 l

Exercícios de Livros Relacionados

O dispositivo mostrado é usado para testar molas de válvula de motor de automóvel. A chave de torque está diretamente conectada ao braço O B . A especificação para a mola da válvula de admissão automo
Um balancim com roletes em A e B é mostrado na posição quando a válvula está aberta e a mola da válvula totalmente comprimida. Nesta posição, a força da mola é de 900N . Determine a força que o balanc
O pequeno guindaste é montado em um lado da caçamba de uma caminhonete. Para a posição θ = 40 ° determine a magnitude da força suportada pelo pino em O e a pressão do óleo p contra o pistão de 50m m d
Calcule as forças normais associadas aos pares de rodas dianteiras e traseiras da van de 1.600k g com tração dianteira. A seguir, repita os cálculos quando a van (a) subir uma inclinação de 10 % e (b)
O carrinho mostrado é útil no manuseio de tambores de 55 galões. Determine a força F necessária para segurar um tambor na posição mostrada. Você pode desprezar o peso do carrinho em comparação com o p