Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 3.Problemas - Ex. 75

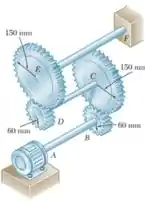
Três eixos e quatro engrenagens são utilizados para formar um trem de engrenagens que transmite 7,5 kW do motor em A para a máquina ferramenta em F. (Os mancais para o eixo são omitidos no esquema) Sabendo que a frequência do motor é de 30 Hz e que a tensão admissível para cada eixo é de 60 MPa, determine o diâmetro necessário em cada eixo.

Passo 1

E ai gurizada tudo belezinha? O enunciado nos pede que a gente determine o diâmetro necessário em cada eixo. Então gurizada o enunciado nos fornece os seguintes dados:

P = 7 , 5   k W   = 7 , 5 × 10 3 W τ a l l = 60   M P a = 60 × 10 6 P a

Começamos a determinar os diâmetros de cada eixo individualmente.

Para o eixo AB temos a seguinte frequência f A B = 30   H z e o torque pode ser determinado como:

T A B = P 2 π f A B = 7 , 5 × 10 3 2 π 30 = 39 , 789   N / m

Para determinarmos o diâmetro temos que partir da equação abaixo

τ = T C A B J A = 2 T π c A B 3 = c A B 3 = 2 T π τ

Substituindo os valores temos:

c A B 3 = 2 39 , 789 π 60 × 10 6 = 422 , 17 × 10 - 9 m 3

c A B = 7.50 × 10 - 3 m = 7 , 50   m m

Agora sim podemos determinar o diâmetro para a seção AB 0/

d A B = 2 c A B = 2 7 ,   50 = 15   m m

Passo 2

Agora gurizada seguindo a mesma lógica devemos determinar o raio na seção CD, vem comigo :D

No Eixo CD temos que determinar a frequência da seguinte maneira

f C D = r B r C f A B = 60 150 30 = 12   H z

Agora podemos determinar o torque nessa seção

T C D = P 2 π f C D = 7.5 × 10 3 2 π 12 = 99.472   N / m

τ C D = T C C D J C D = 2 T π c C D 3 = c C D 3 = 2 T C D π τ

c C D 3 = 2 99.472 π 60 × 10 6 =   1.05543 × 10 - 6 m 3

c C D = 10.18 × 10 - 3 m = 10.18   m m

Agora podemos enfim determinar o diâmetro dessa seção

d C D = 2 c C D = 2 10.18 = 20.4   m m

Passo 3

Gurizada não desistam falta pouco precisamos determinar o diâmetro da última seção

Temos que calcular a frequência para o Eixo EF

f E F = r D r E f E F = 60 150 12 = 4 , 8   H z

Agora podemos determinar o torque nessa seção

T E F = P 2 π f E F = 7.5 × 10 3 2 π 4 , 8 = 248 , 48 .   N / m

τ = T C E F J E F = 2 T π c E F 3 = c E F 3 = 2 248.68 π 60 × 10 6 = 2 , 6886 × 10 - 6 m 3

c E F = 13 ,   82 × 10 - 3 m = 13 , 82   m m

Agora podemos enfim determinar o diâmetro dessa seção

d E F = 2 c E F = 2 13 , 82 = 27 , 6   m m

Resposta

  1. eixo AB d A B = 15.00   m m

  2. eixo CD d C D = 20.4   m m

  3. eixo EF d E F = 27.6   m m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um eixo de acionamento de aço ( G = 77G P a ) tem 2,4m de comprimento e seus diâmetros externo e interno são, respectivamente, iguais a 63,5m m e 57m m . Sabendo-se que o eixo transmite 200h p , a uma
Os dois eixos maciços e as engrenagens mostradas são usadas para transmitir 12k W de um motor em A , que gira a uma frequência de 20H z , a uma máquina-ferramenta em D . Sabendo-se que a máxima tensão
Dois eixos maciços e as engrenagens mostradas são usadas para transmitir 12k W de um motor em A , que gira a uma frequência de 20H z , a uma máquina-ferramenta em D . Sabendo-se que cada eixo tem um d
Sabendo-se que o eixo escalonado mostrado transmite um torque de intensidade T = 280N ⋅ m , determinar a máxima tensão de cisalhamento no eixo, quando o raio de adoçamento é: (a)r = 0,8m m
Sabendo-se que a tensão de cisalhamento admissível é de 55M P a para o eixo escalonado mostrado, determinar a intensidade T do maior torque que pode ser transmitido pelo eixo, quando o raio de adoçame