Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 117

a barra de aço ABC está rigidamente conectada aos suportes e livre de tensões à temperatura de 25°C. O aço é considerado elastoplástico, com E = 200   G P a   e   σ E = 250   M P a . A temperatura de ambas as partes da barra é incrementada ate 150°C. Sabendo que a = 11,7   x   10 - 6 / ° C , determine (a) a tensão em ambas as partes da barra e (b) o deslocamento do ponto C.

Passo 1

Falai aí galera tudo belezinha? O enunciado pede para que a gente determine a tensão em ambas as partes da barra e o deslocamento do ponto C, antes de isso vamos esboçar o diagrama de corpo livre.

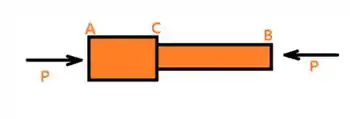
Vamos trazer os dados fornecidos pela questão, vem comigo :D

A A C = 500   x   10 - 6 m 2             L A C = 0,150   m A C B = 300   x   10 - 6 m 2             L C B = 0,250   m                

Considere que: δ p + δ T = 0

Determine ∆ T para causar escoamento na porção CB.

- P L A C E A A C - P L C B E A C B L A B α   x   ∆ T ∆ T = P L A B E α   x   L A C A A C + L C B A C B

Onde:

P = P Y = A C B σ Y = 300   x   10 - 6   x   2,50   x   10 6 = 75   x   10 3 N ∆ T Y = P Y L A B E α   x   L A C A A C + L C B A C B = 75   x   10 3 0,400   x   200   x   10 9   x   11,7   x   10 - 6   x   0,150 500   x   10 - 6 + 0,250 300   x   10 - 6 = 90,812 ° C

Temos então:

T : 150 ° C - 25 ° C = 125 ° C > ∆ T Y

Passo 2

Gurizada falta pouco, vamos considerar que ∆ T > ∆ T Y ,         P = P Y = 75   x   10 3 N podemos então determinar as coisitas pedidas no enunciado 😉

(a) σ A C = - P Y A A C = 75   x   10 3 500   x   10 - 6 = - 150   x   10 - 6 P a σ C B = - P Y A C B = - σ Y

(b) Para ∆ T > ∆ T Y ,porção AC permanece elástica.

δ C / A = - P Y L A C E A A C + L A C α   x   ∆ T = - 75   x   10 3   x   0,150 200   x   10 9   x   500   x   10 - 6 + 0,150   x   11,7   x   10 - 6   x   125 = 106,9   x   10 - 6 m  

Uma vez que o ponto A é estacionário, δ C = δ C / A = 106,9   x   10 - 6 m  

Resposta

  1. σ A C = - 150,0   M P a

    2. σ C B = - 250   M P a

  2. δ C = 0,1069   m m →
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolva o problema 11.48 assumindo que a coluna AB seja rotacionada de 90° em relação ao seu eixo longitudinal.
Um tubo de alumínio com a seção transversal mostrada é atingido diretamente na sua seção média por um bloco de 6kg movendo-se na horizontal com uma velocidade de 2m/s. Utilizando E = 70 GPa, determine
Resolva o prob. 11.50 assumindo que o tubo seja substituído por uma barra maciça de alumínio com as mesmas dimensões externas que as do tubo.
O bloco D de 2 kg cai da posição mostrada sobre a extremidade de uma barra de 16mm de diâmetro. Sabendo que E = 200 GPa, determine (a) a deflexão máxima na extremidade A, (b) o momento fletor máximo n
11.53 O bloco D de 10kg é solto desde uma altura h = 450 mm sobre uma viga de alumínio AB. Sabendo que E = 70 GPa, determine (a) a máxima deflexão do ponto E, (b) a máxima tensão na viga.