Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 4.Problemas de Revisão - Ex. 201

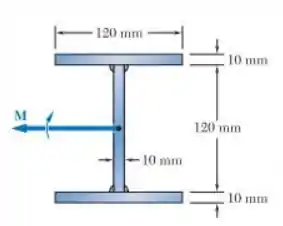
Três placas de aço de 120   m m × 10   m m foram soldadas para formar a viga mostrada na figura. Considerando que o aço seja elastoplástico com E = 200   G P a e σ E = 300   M P a , determine ( a ) o momento fletor para o qual as zonas plásticas na parte de cima e debaixo da viga tenham a espessura de 40   m m e ( b ) o raio de curvatura correspondente da viga.

Passo 1

Fala aí, galera. Beleza? Bora resolver mais um exercício pra tirar aquele notão.

Primeiro, temos que determinar o momento fletor para o qual as zonas plásticas na parte de cima e debaixo da viga tenham a espessura de 40   m m . Para isso, vamos dividir nossa viga em 3 partes:

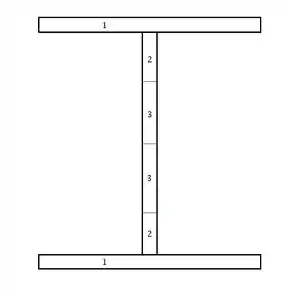
Em seguida, vamos calcular a área para cada parte:

A 1 = 120 10 A 1 = 1200   m m 2

A 2 = 30 10 A 2 = 300   m m 2

A 3 = 120 10 A 3 = 1200   m m 2

E então, vamos encontrar as resultantes. Para isso, devemos usar a seguite relação:

σ y = R A

Substituindo para cada área, temos:

R 1 = σ y A 1 = 300 × 10 6 1200 × 10 - 6 R 1 = 3 6 0 × 10 3   N

R 2 = σ y A 2 = 300 × 10 6 3 00 × 10 - 6 R 2 = 90 × 10 3   N

R 3 = 1 2 σ y A 2 = 1 2 300 × 10 6 300 × 10 - 6 R 3 = 45 × 10 3   N

O último passo para calcularmos o momento fletor dado que a viga tenha uma espessura de 40   m m é a distância para a linha neutra para as três partes. Temos:

y 1 = 65 × 10 - 3   m y 2 = 4 5 × 10 - 3   m y 3 = 20 × 10 - 3   m

Agora é só calcular o momento fletor. Ele é dado por:

M = 2 R 1 y 1 + R 2 y 2 + R 3 y 3 M = 2 360 × 10 3 65 × 10 - 3 + 90 × 10 3 45 × 10 - 3 + 45 × 10 3 20 × 10 - 3 M = 56,7   k N ∙ m

Passo 2

Em seguida, vamos encontrar o raio de curvatura correspondente para a viga. Ele é dado por:

y y ρ = σ y E ρ = E y y σ y ρ = 200 × 10 9 30 × 10 - 3 300 × 10 6 ρ = 20   m m

É isso, galera!!! Bora zerar esse livro?

Resposta

M = 56,7   k N ∙ m

ρ = 20   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sabendo que P = 90k s i , determine a maior distância a para qual a tensão máxima de compressão não excede 18k s i .
Sabendo que a = 1,25i n , determine o maior valor de P que pode ser aplicado se exceder as tensões admissíveis a seguir: σ t r a ç ã o = 10k s i çã σ c o m p r e s s ã o = 1 8k s i ã
Uma força horizontal P de intensidade 100kN é aplicada à viga mostrada na figura. Determine a maior distância para a qual a tensão de tração máxima na viga não ultrapasse 75 M p a .
O tubo mostrado na figura tem parede com espessura constante de 12mm. Para o carregamento dado, determine.O ponto em que a linha neutra intercepta a linha ABD.
Uma placa rígida circular com raio de 125m m está presa a um poste retangular cheio de 150 x 200m m , com o centro da placa alinhado ao centro do poste. Se uma força Pd e4 k N for aplicada a E com θ =