Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas - Ex. 22
Dois elementos de seção transversal uniforme de são colados entre si ao longo do plano que forma um ângulo de com a horizontal. Sabendo que as tensões admissíveis para a junta colada são e determine a maior força centrada que pode ser aplicada.
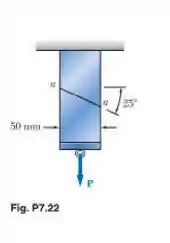
Passo 1
Fala aí, galerinha. Tudo bem com vocês?
Nesta questão, sabemos que no plano
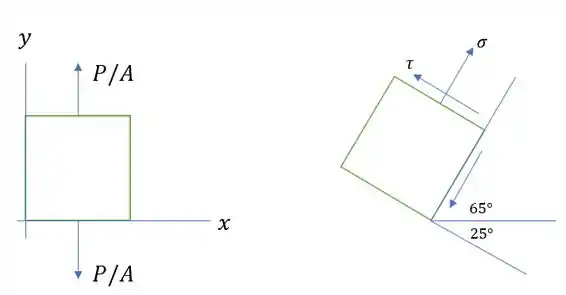
Também sabemos que:
Passo 2
Agora, vamos utilizar os dados acima para achar a força. Sabemos que a tensão normal é dada por:
Isolando
Para a tensão cisalhante, temos que:
Isolando
Devemos escolher o menor valor, para que não ultrapassemos a tensão limite. Logo:
Resposta
Exercícios de Livros Relacionados
O tubo de extremidade aberta tem parede de espessura 2 mm e diâmetro interno de 40 mm. Calcule a pressão que o gelo exerceu na parede interna do tubo para provocar a ruptura mostrada na figura. A tens
Inicialmente, a cinta de aço inoxidável 304 está perfeitamente ajustada em torno do cilindro rígido liso. Se ela for submetida a uma queda de temperatura não linear ΔT = 12sen²θ ºC, onde θ é dado em r
Sabendo que o tubo estrutural mostrado tem parede de espessura constante de 6,35 mm, determine as tensões normal e de cisalhamento nos três pontos indicados.
Para o poste e o carregamento mostrados na figura, determine as tensões principais, os planos principais e a tensão de cisalhamento máxima no ponto H.
O tubo estrutural mostrado na figura tem uma parede de espessura uniforme de 7,62mm. Sabendo que a força de 66,7kN é aplicada 3,8mm acima da base do tubo, determine a tensão de cisalhamento ( a ) no p