Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas - Ex. 106

Três placas são soldadas juntas para formar a viga mostrada. Sabendo-se que σ a d m = 150   M P a , determinar a mínima largura b do flange que pode ser utilizado.

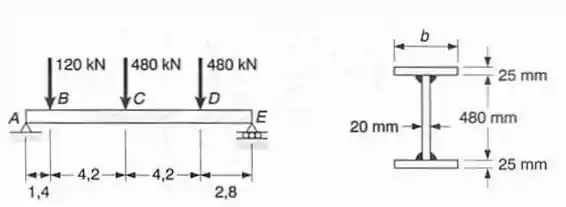
Passo 1

Oi, fala aí, galerinha!!! Para resolver esse problema a gente vai seguir o seguinte passo a passo:

  1. Calcular as reações em A e E por meio das equações da estática.
  2. Calcular a força cortante, o momento fletor e achar o momento fletor máximo.
  3. Calcular o módulo resistente ( W ) mínimo que a seção deve possuir.
  4. Calcular o módulo resistente da seção em função de b e comparar com o valor do item anterior.

Perceba que agora temos de fazer três testes depois da escolha do nosso perfil!

Então partiu pro exercício!

Passo 2

Para facilitar fazer um desenho das forças:

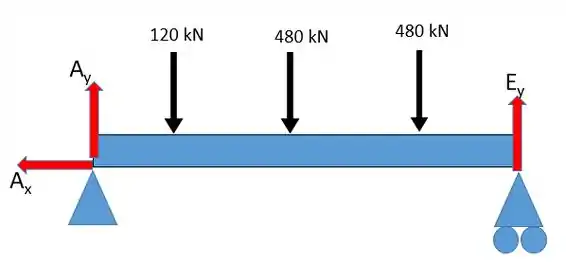
Agora vamos calcular as reações. Primeiro vamos perceber que não existem forças horizontais além de A x , logo, esta é nula. Com isso vamos partir para o somatório das forças em y :

∑ F y = 0

A y - 120 - 480 - 480 + E y = 0

A y + E y = 1080   k N

E finalmente o somatório dos momentos:

∑ M A = 0

- 120 × 1,4 - 480 × 5,6 - 480 × 9,8 + E y × 12,6 = 0

E y = 600   k N

Substituindo na equação anterior

A y = 1080 - 600 = 480   k N

Passo 3

Nós queremos o máximo momento fletor máximo e a força cortante máxima. Então temos de pegar o ponto onde a cortante é nula, nesse ponto o momento fletor é máximo. A força cortante nula ocorre em x = 5,6   m , observe:

V x = 5,6 m = 480 - 360 - 120 = 0

Agora podemos calcular o momento fletor máximo:

M m á x = 120 × 1,4 + 480 × 4,2

M m á x = 2184   k N . m

Passo 4

Agora vamos achar o momento resistente mínimo que a viga deve possuir W m í n , que é dado por:

W m í n = M m á x σ a d m

W m í n = 2184 × 10 3   1 5 0 × 10 6

W m í n = 14,56 × 10 - 3   m 3 = 14560 × 10 3   m m 3

Passo 5

Agora vamos fazer o cálculo do momento resistente, em função de b :

W = I c

O momento de inércia I é calculado a soma de três momentos um relativo a cada barra. Lembrando que o momento de uma barra é dado por:

I 0 = b h 3 12

Assim como o teorema dos eixos paralelos:

I = I 0 + A d 2

Onde A é a área e d a distância entre o centro da barra ao eixo de rotação.

Agora vamos calcular cada momento de inércia:

I 1 = I 3 = 1 12 × b × 0,025 3 = b   .   1,3021 × 10 - 6   m 4

I 2 = 1 12 × 0,020 × 0,480 3 = 1,8432 × 10 - 4   m 4

Mas com relação às barras superior e inferior temos de aplicar o teorema dos eixos paralelos:

I 1 = I 3 = b   .   1,3021 × 10 - 6 + ( b × 0,025 × 0,2525 )

I 1 = I 3 = b × 7,6146 × 10 - 3   m 4

Logo a seção, como um todo, tem o momento de inércia de:

I = I 1 + I 2 + I 3

I = 1,8432 × 10 - 4 + 0,01523 b

Como queremos W , basta dividir por c que é a altura da linha neutra c = 0,2525   m

W = 1,8432 × 10 - 4 + 0,01523 b 0,2525

Agora é só igualar isso a W m í n = 14560 × 10 3   m m 3

Mas antes temos de passar para m 3

W m í n = 14560 × 10 - 6   m 3

Passo 6

Igualando:

1,8432 × 10 - 4 + 0,01523 b 0,2525 = 14560 × 10 - 6

0,01523 b = 3,49208 × 10 - 3

b = 230   m m

Resposta

b = 230   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se a tensão de apoio admissível para o material sob os apoios em A e B for σ aa d m =2,8M P a , determine a carga P máxima que pode ser aplicada à viga. As seções transversais quadradas das chapas de
A lança é suportada pelo cabo do guincho com diâmetro de 6m m com tensão normal admissível σ a d m = 168 M P a . Se a lança tiver de levantar lentamente uma carga de 25 k N , de θ = 20 ° até θ = 50 °
Determine a área da seção transversal exigida para o elemento B C e os diâmetros exigidos para os pinos em A e B se a tensão normal admissível for σ a d m=21M P a e a tensão de cisalhamento for τ a d
O conjunto consiste em três discos A ,BeC usados para suportar a carga de 140k N . Determine o menor diâmetro d 1 do disco superior, o diâmetro d 2 do espaço entre os apoios e o diâmetro d 3 do orifíc
Se a tensão de apoio admissível para o material sob os apoios em A e B for σ a a d m=2,8M P a , determine os tamanhos das chapas de apoio quadradas A ' e B ' exigidos para suportar a carga. A dimensão