Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 11.Problemas - Ex. 44b
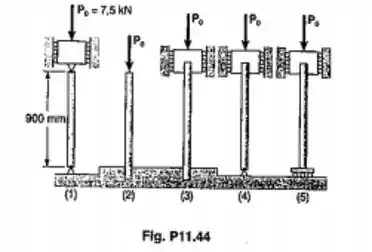
Cada uma das cinco colunas mostradas consiste de uma barra maciça de aço. Pede-se(a) sabendo-se que a coluna da Fig(1) tem 20mm de diâmetro, determinar o coeficiente de segurança em relação a flambagem para o comprimento mostrado;(b) determinar o diâmetro em cada uma das outras estruturas, para que o coeficiente de segurança seja o mesmo que o coeficiente de segurança obtido na parte a. Usar E=200GPa.
Passo 1
E aí, vamo partir pra esse item b?
Bom, com o fator de segurança encontrado a gente pode seguir, aqui a gente precisa do diâmetro de cada uma das colunas, aqui a gente vai usar a fórmula do peso crítico considerando o coeficiente de flambagem que é dada por:
O diâmetro está implícito no momento de inércia que pra seção circular é dado por:
E após isso comparar com o peso admissível lembrando que:
Para encontrar cada um dos coeficientes vamos analisar as condições de contorno de cada uma das 4 colunas olhando pra figura.
Os retângulos azuis indicam onde estão os engastes, a elipse vermelha indica um apoio do tipo pino e a elipse amarela indica um rolete ou carrinho o círculo verde mostra a extremidade livre. Então vamos a análise para encontrarmos os coeficientes de flambagem .
(2) Possui uma extremidade engastada e outra livre o que configura um coeficiente
(3) Possui duas extremidades engastadas o que nos dá um coeficiente
(4) Possui uma extremidade engastada e outra rotulada o que configura um coeficiente
(5) Possui uma extremidade engastada e outra com um rolete o que configura um coeficiente
Passo 2
Bom, com a análise feita podemos pensar numa boa relação pro diâmetro, como o fator de segurança vai ser o mesmo para cada coluna e temos o mesmo peso admissível, a gente vai ter o mesmo peso crítico e podemos então encontrar uma relação para o momento de inércia e no fim alterar os valores de para cada caso.
Isolando o I, teremos:
E sabemos que:
Então:
E aqui tem uma parada interessante, como tooodos os valores são os mesmos exceto o valor de e , podemos dizer que há uma relação entre e os demais, e como podemos dizer que:
Passo 3
Agora que encontramos a fórmula que relaciona os momentos de inércia podemos ganhar um bom tempo na nossa resolução, então vamos partir para o cálculo dos diâmetros.
Lembrando que:
Então temos para a coluna 2 que possui
E para achar o diâmetro isolamos da seguinte forma:
Daí, temos:
Seguindo para as outras colunas vamos fazer o mesmo processo, e para coluna 3 que possui .
E pela relação encontrada pro diâmetro podemos dizer que:
Para coluna 4 que possui .
E pela relação encontrada pro diâmetro podemos dizer que:
E como a última coluna possui as mesmas condições de contorno da primeira, mesmo comprimento tipo de seção e também é feita do mesmo material podemos dizer que:
Resposta
(b)