Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 6.Problemas - Ex. 43
Três tábuas são conectadas por parafusos com in de diâmetro com espaçamento longitudinal de 6 in. ao longo do eixo longitudinal da viga. Para uma força cortante vertical na viga igual a 2,5 kips, determine a tensão de cisalhamento média nos parafusos.
Passo 1
E ai gurizada tudo belezinha? O enunciado pede que a gente determine a tensão de cisalhamento média nos parafusos, então vamos começar esboçando o elemento e posteriormente calculando a área, vem comigo :D
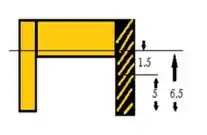
Passo 2
Agora partiu determinar a inércia do elemento, vem comigo ;)
+
Agora vamos determinar a força ;)
Agora sim podemos determinar a tensão:
Resposta
Exercícios de Livros Relacionados
Para a viga com o carregamento indicado, considerar a seção n - n e determinar a tensão de cisalhamento no: (a) ponto a ; (b) ponto b .
Determinar a maior tensão de cisalhamento, na seção n - n .
Determinar a maior tensão de cisalhamento na seção n - n .
Para a viga em balanço e o carregamento dado, determinar o ponto onde a tensão de cisalhamento é mázima e o corresponde valor da tensão: (b) ao longo da linha D ' E ' de uma perna.
Determinar a localização do centro de cisalhamento O de uma viga de parede fina de espessura uniforme e com a seção transversal mostrada.