Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 6.Problemas - Ex. 77

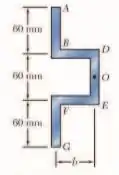
Uma viga de paredes finas de espessura uniforme tem a seção transversal mostrada na figura. Determine a dimensão b para a qual o centro de cisalhamento O da seção transversal está localizado no ponto indicado.

Passo 1

E ai gurizada tudo bem? O enunciado pede que a gente determine a dimensão b para a qual o centro de cisalhamento O da seção transversal está localizado no ponto indicado. Para isso vamos esboçar o diagrama de corpo livre, vem comigo :D

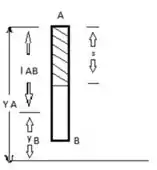
Na Parte AB temos:

A s = t s           y - s = y A - 1 2 s

Q s = A s y - s = t y A s - 1 2 t s ²

q s = V Q s I = V t I   y A s - 1 2 t s ²

Considere as forças sobre os pontos esboçados abaixo :D

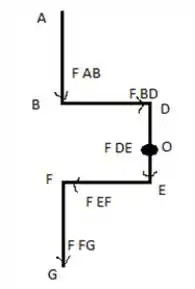
Temos então:

F =   ∫ 0 l A B q s d s = V t I   y A l A B 2 2 -   l A B 3 6 ↓

Passo 2

Consideramos a seção em B, então vejam este esboço para entendermos melhor :D

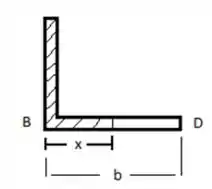
Temos então:

Q B = t y A l A B - 1 2 t l A B 2

Por simetria,

F F G = F A B

Parte BD:

A x = t x

Q x = Q B + y B A x = Q B + t y B x

q x = V Q x I = V I ( Q B + t y B x )

F B D =   ∫ 0 b q x d x = V I   Q B b + 1 2 t y B b ²

Passo 3

Por simetria, consideramos:

F E F = F B D

F D E não é requerido, a partir que seu momento sobre O é zero.

↺ Σ M O = 0 :             b F A B + F F G - y B F B D +   y F F E F = 0

2 b   F A B - 2 y B F B D = 0

2 b ∙ V t I     y A l A B 2 2 - l A B 3 6 - 2 y B V 1   Q B b + 1 2 t y B b 2 = 0

2 V t I 1 2     y A l A B 2 - 1 6   l A B 3   b -   2 V t I y A l A B - 1 2 l A B 2 y B b - 1 2 y 2 B b 2 = 0

Passo 4

Dividindo por 2 V t I e substituindo dados numéricos,

1 2 90 60 2 - 1 6 ( 60 ) ³ b - 90 60 - 1 2 60 2 30 b + 1 2 30 2 b 2 = 0

126 × 10 3 b - 108 × 10 3 b + 450 b 2 = 0

18 × 10 3 b - 450 b 2 = 0

b = 0   e   b = 40,00   m m

Resposta

b = 0   e   b = 40,00   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a localização do centro de cisalhamento O de uma viga de paredes finas de espessura uniforme com o seção transversal mostrada.
Resolva o problema 6.83, considerando que uma placa de 6m m de espessura é dobrada para formar o U mostrado.
Uma placa de aço, com 160m m de largura e 8m m de espessura, é dobrada para formar a viga em forma de U mostrada na figura . Sabendo que a força vertical P atua em um ponto do plano médio da alma do U
Para a barra composta indicada, determine o maior momento fletor admissível quando a barra é flexionada em torno do eixo vertical. Barra do problema 4.33 .
Uma barra com a seção transversal mostrada na figura foi construída unindo-se firmemente latão e alumínio. Usando os dados fornecidos abaixo, determine o maior momento fletor admissível quando a barra