Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 23

Para a viga com o carregamento indicado, considerar a seção n - n e determinar a tensão de cisalhamento no: (a) ponto a ; (b) ponto b .

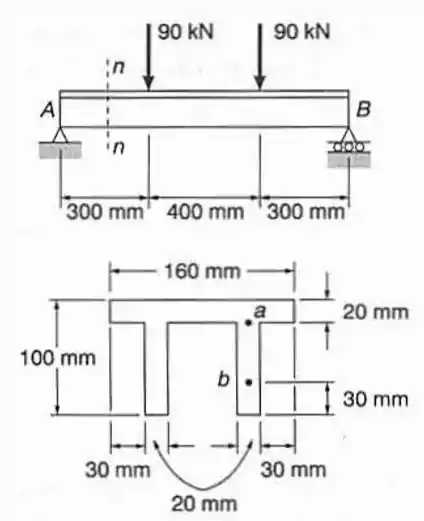
Passo 1

O problema pede a tensão de cisalhamento nos pontos a e b , logo vamos ter que utilizar o famoso “tau vê qit”

τ = V Q I t

Desta forma nós queremos o τ que é a tensão cisalhante, para isso vamos achar a força cortante V . Além da geometria da figura, que por meio da geometria vamos achar o momento de inércia I , o momento estático Q e a espessura t .

Passo 2

Vamos utilizar a geometria da figura para achar o momento de inércia. Antes de achar o momento de inércia precisamos saber a posição da linha neutra Y -

Y - = ∑ A ⋅ y - ∑ A

Y - = 20 ⋅ 80 ⋅ 40 + 20 ⋅ 80 ⋅ 40 + 160 ⋅ 20 ⋅ 90 20 ⋅ 80 + 20 ⋅ 80 + 160 ⋅ 20

Y - = 65   m m

Agora podemos calcular o momento de inércia:

I = I 1 + 2 ⋅ I 2

I 1 = 1 12 b h 3 + A d ²

I 1 = 1 12 ⋅ 0 , 16 0 ⋅ 0,02 0 3 + 0,16 0 ⋅ 0,02 0 ⋅ 0,0 2 5 ²

I 1 = 2,1 × 10 - 6   m 4

I 2 = 1 12 b h 3 + A d ²

I 2 = 1 12 ⋅ 0,020 ⋅ 0,08 0 3 + 0,02 0 ⋅ 0,08 0 ⋅ 0,025 ²

I 2 = 1,86 × 10 - 6   m 4

I = 2,1 × 10 - 6 + 2 ⋅ 1,86 × 10 - 6

I = 5,82 × 10 - 6   m 4

Passo 3

Agora vamos ter que achar a força cortante por meio da carga aplicada à barra, primeiro vamos achar a reação em A aplicando o momento no ponto B :

∑ M B = R A ⋅ 1000 - 90 ⋅ 700 - 90 ⋅ 300 = 0

R A = 90 ⋅ 700 + 90 ⋅ 300 1000 = 90   k N

Como o corte n - n está antes da força de 90   k N então a força cortante tem o mesmo valor da reação em a :

V = 90   k N

Passo 4

Agora que muda um pouco a letra a em relação à letra b porque o momento estático vai mudar um pouquinho, olha só como fica para a letra a onde pegamos a parte de cima para o cálculo:

Q = ∑ A ⋅ y -

Q a = 0,160 ⋅ 0,02 0 ⋅ 0,025

Q a = 8 × 10 - 5   m 3

Já para a letra b é mais simples pegar a parte de baixo:

Q b = 2 ⋅ ( 0,020 ⋅ 0,03 0 ⋅ 0,050 )

Q b = 6 × 10 - 5   m 3

Passo 5

Agora é só substituir na nossa formulinha como falado no primeiro passo! Para a letra a

τ = V Q I t

Onde t é a espessura t = 40   m m .

τ = 90 000 ⋅ 8 × 10 - 5   5,82 × 10 - 6 ⋅ 0,0 40

τ = 30,72   M P a

Passo 6

Para a letra b :

τ = V Q I t

Onde t é a espessura t = 40   m m .

τ = 90 000 ⋅ 6 × 10 - 5 5,82 × 10 - 6 ⋅ 0,0 40

τ = 23   M P a

Resposta

a)

τ = 30,72   M P a

b)

τ = 23   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga de alumínio extrudada tem espessura de parede constante de in. Sabendo que a força cortante vertical na viga é de 2 kips, determine a tensão de cisalhamento correspondente em cada um dos cinco
Quatro cantoneiras de aço 1,202 x 102 x 9,5 e uma placa de 12 x 400 mm são parafusadas de modo a formar a viga de seção transversal mostrada. Os parafusos tem diâmetro de 22mm e são espaçados longitud
Saber que um determinado cisalhamento vertical V causa uma tensão de cisalhamento máxima de 75 MPa em uma viga extrudada tendo a seção transversal mostrada, determine o tensão de cisalhamento nos três
Uma coluna é fabricada conectando-se os perfis de aço laminado mostrados na figura por parafusos de 19,05 mm de diâmetro espaçados longitudinalmente a cada 190,5 mm. Determine a tensão de cisalhamento
Três tábuas, cada uma com 50,8 mm de espessura, são pregadas entre si para formar uma viga que está submetida a uma força cortante vertical. Sabendo que a força cortante admissível em cada prego é de