Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 1.Problemas - Ex. 36

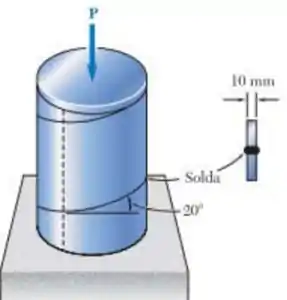
Um tubo de aço de 400 mm de diâmetro externo é fabricado a partir de uma chapa de aço com 10 mm de espessura, soldada ao longo de uma hélice que forma um ângulo de 20° com um plano perpendicular ao eixo do tubo. Sabendo que as tensões normal e de cisalhamento máximas admissíveis nas direções respectivamente, normal a tangencial à solda são σ = 60 M P a e τ   = 36   M P a , determine o valor P da maior força axial que pode ser aplicada ao tubo.

Passo 1

  1. E ai gurizada tudo belezinha??? Vamos analisar o elemento e partiu calcular a área primeiramente :D

    2. d o = 0,4   m

    r o = d o 2 = 0,4 2 = 0,2   m

    r i = r o - t = 0,2 - 0,01 = 0,19   m

    A o   = π r o 2 - r i 2 = π 0,2   2 - 0,19 2 = 12 , 25 × 10 - 3   m ²

    Sabendo que a equação da tensão é apresentada abaixo para um ângulo de 20°, então vamos achar “P” :D

    σ = P   c o s ²   θ A

    60 × 10 6 = P     c o s ²   20 12,25 × 10 - 3

    P = 832,52   × 10 3   N = 832,52   N

    Passo 2

  2. a pressão de cisalhamento que atua na superfície com um ângulo de 40°

36 × 10 6   = P   s e n   40 2 × 12,25 × 10 - 3

P   = 1372,4   × 10 3   N = 1372,4     K N

Resposta

1372,4     K N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolver o problema 7,121 considerando que a carga uniformemente distribuída é substituída por uma carga concentrada de 250 KN, no centro do vão de 6 m.
Determinar o valor admissível de P para o carregamento mostrado, sabendo-se que σ adm= +55 MPa na tração e σadm= -125 MPa na compressão, e tadm= 30 MPa .
Resolver o problema 7.117 assumindo o perfil laminado T da viga é invertido.
Uma carga uniformemente distribuída de 66 KN/m deve ser suportada pelas vigas AB e CD, como mostrado. Sabendo-se que σadm = 140 MPa e t adm= 85 MPa, determinar: a) o menor comprimento admissível L da
A viga AB tem uma seção transversal retangular de largura b constante e altura h variável. Sabendo que a viga deve ser de resistência constante, expressar h em termos de x, L e ho.