Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas - Ex. 117

Determinar o valor admissível de P para o carregamento mostrado, sabendo-se que σ adm= +55 MPa na tração e σadm= -125 MPa na compressão, e tadm= 30 MPa .

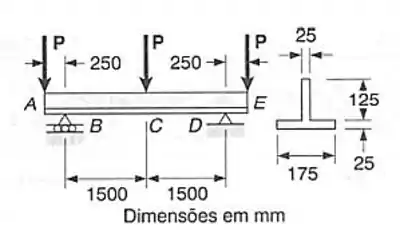
Passo 1

E ai gurizada tudo belezinha??? Partiu calcular valor admissível de P para que?? Vem comigooo!!

Para isso vamos que:

∑ M b = F × d

M b = P × 0,25

7,53 = P × 0,25

P = 30,15   K N

∑ M c = V A × 1,5 - P × 1,75 (1)

∑ M d = V A × 3 - 1,5 × P - 1 , 7 5 × P + 0,25 ×   P

V A = 1,5 P (2)

Subtituindo 2 em 1 temos:

∑ M c = 1,5   P × 1,5 - P × 1,75 (3)

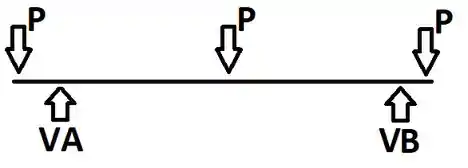
Gurizada para acharmos o momento no centro da viga, calcularemos da seguinte maneira:

σ = m × c I x

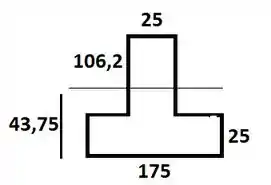
Galera lembrando que a inércia é tabelada então temos...

55 = m × 43,75 14550781

m = 17,13   K N m

Substituindo esse valor do momento na equação 3 temos...

17,13 = 1,5   P × 1,5 - P × 1,75

P = 34,26   K N

Resposta

P = 34,26   K N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Refaça o problema 7.179 considerando a barra invertida.
Para a viga com o carregamento mostrado, desenhar os diagramas de cortante e de momento fletor, e dimensionar a seção transversal da viga, sabendo-se que σ a d m = 8,6M P a e τ a d m = 0,62M P a .
A força transversal P é aplicada, como mostrado, na extremidade A de um tronco de cone A B . Denotando por d 0 o diâmetro em A , mostre que a máxima tensão normal ocorre no ponto H , que está contido
Uma barra maciça de aço tem uma seção transversal trapezoidal e suporta uma carga uniformemente distribuída w como mostrado. Sabendo-se que σ a d m = + 75 M P a na tração e σ a d m = - 100 M P a na co
Sabendo-se que σ a d m = 160 M P a e τ a d m = 100 M P a , selecionar o perfil de abas largas que poderá ser usado para suportar o carregamento mostrado.