Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 3.Problemas de Revisão - Ex. 151
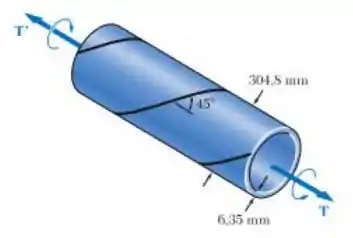
Um tubo de aço com diâmetro externo de 304,8 mm é fabricado a partir de uma chapa de 6,35 mm de espessura usando-se solda ao longo de uma linha helicoidal que forma um ângulo de 45° com o plano perpendicular ao eixo do tubo. Sabendo que a máxima tensão de tração na solda é de 82,7 MPa, determine o maior torque que pode ser aplicado nesse tubo.
Passo 1
E ai gurizada tudo belezinha? O enunciado pede que a gente determine o maior torque que pode ser aplicado nesse tubo. Então vamos começar desenhando o diagrama de corpo livre, vem comigo :D
Sabendo que:
Consequentemente:
Agora podemos achar J :D
Agora podemos determinar o torque a partir da equação abaixo :D
Resposta
Exercícios de Livros Relacionados
A turbina desenvolve 150k W de potência, que é transmitida às engrenagens de tal modo que C e D recebem quantidades iguais. Se a rotação do eixo de aço A-36 de 100m m de diâmetro for ω=500r e v / m i
A turbina desenvolve 150k W de potência, que é transmitida às engrenagens de tal modo que C recebe 70% e D recebe 30%. Se a rotação do eixo de aço A-36 de 100m m de diâmetro for ω =800r e v / m i n u
O motor produz um torque T = 20N . m na engrenagem A . Se a engrenagem C travar repentinamente e parar de girar, mas B puder girar livremente, determine o ângulo de torção de F em relação a E e de F e
O motor transmite 33k W ao eixo de aço inoxidável 304 quando gira a 20H z . O eixo tem diâmetro de 37,5m m e está apoiado em mancais lisos em A e B , que permitem a livre rotação do eixo. As engrenage
O motor transmite 33k W ao eixo de aço inoxidável 304 quando gira a 20H z . O eixo é apoiado em mancais lisos em A e B , que permitem a livre rotação do eixo. As engrenagens C e D presas ao eixo absor