Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 13

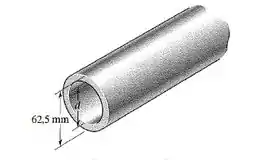
Um tubo de aço com diâmetro externo de 62,5   mm é usado para transmitir 3   kW quando gira a 27   rev/minuto . Determine, com aproximação de múltiplos de 5   mm , o diâmetro interno d do tubo se a tensão de cisalhamento admissível for τ a d m = 70   Mpa

Passo 1

Oláaaa! Tá bem? Bora entender o que está acontecendo!

Um tubo de aço transmite P = 3   kW sob uma frequência de f = 27   rev/minuto . Essa transmissão gera um torque no tubo. A torção exercida no tubo vai induzir tensões cisalhantes! O tubo só pode sofrer no máximo uma tensão de τ a d m = 70   MPa .

A fórmulinha da tensão de cisalhamento quando se tem torção é

τ = T   r J

Onde T é o torque atuando na seção, r é a distância entre o centro dessa seção e o ponto onde a gente quer a tensão de cisalhamento (na seção) e J é o momento polar de inércia. Como nós temos um tubo, esse último carinha é dado por

J = π r e 4 - r i 4 2

Percebe que quanto maior r maior τ , então a tensão máxima acontece no ponto da seção mais longe do centro, ou seja, na borda do tubo! Essa tensão que deve ser igual a nossa tensão admissível para que o tubo resista ao torque. Logo, r vai ser o raio externo r e do nosso tubo.

τ a d m = τ m á x = T   r e J

A ideia é a gente usar essa fórmulinha e achar o diâmetro interno que esse tubo tem que ter. Bora lá!

Passo 2

Vamos começar achando o momento polar de inércia dado por

J = π r e 4 - r i 4 2

Aí o raio externo é metade do diâmetro externo:

r e = d e 2 = 62,5 2   m m

E o raio interno é metade do diâmetro interno que a gente quer descobrir:

r i = d 2

Substituindo na fórmulinha essas coisas:

J = π 62,5   m m 2 4 - d 2 4 2

J = π 62,5   m m 4 16 - d 4 16 2

J = π 62,5   m m 4 - d 4 32

Passo 3

Falta achar o torque T . Podemos achar a relação entre potência transmitida e torque por essa fórmulinha:

P = 2 π f T

Temos

P = 3   k W

f = 27   rev/minuto  = 27 60   r e v / s

Vamos substituir os valores e já achar que torque é esse! Cuidado com as unidades

3   kW = 2 ⋅ p i ⋅ 27   rev/minuto ⋅ T

T = 3   kW 2 ⋅ p i ⋅ 27 / 60   rev/s = 1,061   kNm

Percebe que a gente precisou passar a frequência f = 27   rev/minuto para r e v / s , a dividindo por 60 , ta?

Passo 4

Segundo a fórmula, a tensão máxima vai ocorrer o mais distante possível do centro, onde r é o raio externo. Então r e = d e / 2 = 31,25   mm . Usando a tensão admissível τ a d m = 70   Mpa na fórmula da tensão:

τ = T   r e J

70   MPa = 1,061   kNm ⋅ 31,25   mm J

J = 4,73660714 ⋅ 10 - 7   m 4 = 473660,714   mm 4

Show! Esse é o momento polar de inércia que o tubo deve ter! Agora podemos achar o diâmetro interno d usando:

J = π 62,5   m m 4 - d 4 32

Substituindo nosso J e isolando d :

473660,714   mm 4 = π 62,5   m m 4 - d 4 32

d = 56,83   mm

Com aproximação de 5   mm como a questão pede:

d = 60   mm

Resposta

Diâmetro interno: d = 60   mm .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um eixo maciço de raio r está sujeito a um torque T . Determine o raio r ' do núcleo interno do eixo que resista à metade do torque aplicado ( T / 2 ). Resolva o problema de duas maneiras: a usando a
O tubo é submetido a um torque de 750 N · m. Determine a parcela desse torque à qual a seção sombreada cinza resiste. Resolva o problema de duas maneiras: (a) usando a fórmula da torção e (b) determin
Um eixo maciço de raio r está sujeito a um torque T . Determine o raio r ' do núcleo interno do eixo que resista a 1 / 4 do torque aplicado ( T / 4 ). Resolva o problema de duas maneiras: a usando a f
Um eixo maciço de 30mm de diâmetro é usado para transmitir os torques aplicados às engrenagens. Determine a tensão de cisalhamento máxima absoluta no eixo.
O eixo tem diâmetro de 80mm e, devido ao atrito na superfície no interior do furo, está sujeito a um torque variável descrito pela função t = 25 x ⋅ e x 2Nm/m , onde x é dado em metros. Determine o to