Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 2
Um eixo maciço de raio está sujeito a um torque . Determine o raio do núcleo interno do eixo que resista à metade do torque aplicado (). Resolva o problema de duas maneiras: usando a fórmula da torção e determinando a resultante da distribuição da tensão de cisalhamento.
Passo 1
Fala, querido!
Um torque está forçando um eixo maciço. Essa questão não tem valores. Vamos anotar tudo que sabemos.
Características do eixo:
- Raio do eixo: .
- Momento polar de inércia: . (Eixo maciço)
Até aqui todas essas letras são conhecidas!
Queremos descobrir o raio que define a parte interna do eixo capaz de resistir .
A questão pede que façamos as contas de duas formas:
- Caso A: usando a fórmula da torção.
- Caso B: usando a resultante da distribuição de tensão de cisalhamento.
Vamos pro Caso A primeiro!
Passo 2
O torque gera uma distribuição de tensão de cisalhamento nas seções do eixo. Começamos com a fórmula da torção:
Imaginando uma seção transversal que vai apenas até , queremos que . Nessa seção imaginária, teríamos . A tensão cisalhante em seria
Beleza! Só não conhecemos o valor de ! Vamos resolver isso.
Passo 3
Sabemos que a tensão de cisalhamento será máxima quando usarmos o raio inteiro do eixo :
E também sabemos que a tensão varia linearmente até de acordo com o raio. Podemos usar algo com o uma semelhança de triângulos. Olha um esboço da distribuição de tensão na seção:
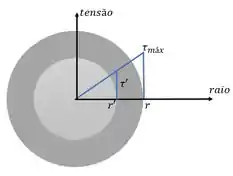
Agora vamos substituir tudo!
Achamos o valor de pelo Caso . Vamos ver agora pelo caso .
Passo 4
Vamos para o caso B.
Temos uma definição que diz que o torque que atua em uma seção de raio é equivalente ao torque resultante da distribuição de cisalhamento até esse raio.
Se pensar bem, isso faz sentido. Num ponto temos um valor de ’. Todo cisalhamento até aquele ponto deve produzir esse valor de torque. Para ficar tudo equilibrado.
Vamos com calma, para o Caso precisamos somar os efeitos de cisalhamento na seção inteira (integral!).
Bem, podemos começar escrevendo
Isso significa que estamos somando as contribuições de torque! Vamos ver como. Esse pequeno torque pode ser causado por uma pequena força atuando a uma distância de um centro de rotação (centro do eixo):
E agora pense o seguinte. Imagine uma área circular bem pequena que está distante do centro e tem espessura (um anel).
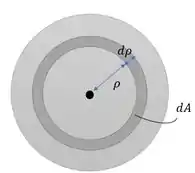
Se a tensão de cisalhamento nessa área for chamada de , temos que a força gerada por essa tensão é
De volta à integral:
Está melhorando! O que essa integral significa é que estamos somando as contribuições de torque em toda a área (a área do eixo até um raio ).
Aquele ali a gente já sabe que está relacionado a ! Vamos continuar
Pra essa integral ficar fácil, a gente quer que ela fique definida segundo comprimentos! Vamos achar a área , achando o comprimento do anel e multiplicando pela espessura que ele tem .
Chegamos finalmente em
A gente coloca de 0 até , porque queremos o torque produzido em .
Passo 5
O que o Caso nos pede é que o torque resultante dessa integral seja .
Fechou! Mesma resposta!
Resposta
Raio: .