Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 2.Problemas - Ex. 28
O material é distorcido até a posição, como mostra a figura. Determine a deformação normal média que ocorre ao longo das diagonais AD e CF.
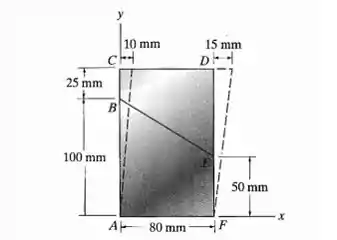
Passo 1
Desenhando, teremos:
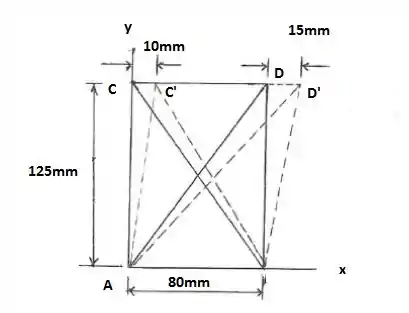
Podemos calcular algumas distâncias:
Passo 2
Podemos então calcular as deformações:
Resposta
Exercícios de Livros Relacionados
O tubo de latão AB E = 105G P a tem área de seção transversal de 144 m m 2 e é ajustado com plugue em A. O tubo está conectado em B a uma placa rígida que, por sua vez, está conectada em C ao fundo de
O pórtico de aço ( E = 200G P a ) mostrado tem a escora diagonal BD com área de 1920 m m 2 . Determine a máxima carga P admissível se a mudança de comprimento do elemento BD não excede 1,6mm.
Os elementos ABC e DEF são unidos por barras de conexão de aço ( E = 200G P a ) . Cada uma dessas barras é feita de um par de placas de 25 x 35 mm. Determine a mudança de comprimento do (a) elemento B
Para a treliça de aço E = 20G P a e o carregamento mostrado, determine as deformações dos componentes AB e AD, sabendo que suas áreas de seção transversal são, respectivamente, 2400 m m 2 e 1800 m m 2
Para a treliça de aço ( E = 200G P a ) e os carregamentos mostrados, determine as deformações dos componentes BD e DE, sabendo que suas áreas de seção transversal são, respectivamente, 1290 m m 2 e 19