Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 4

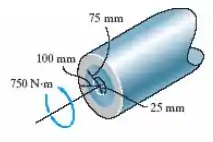
O tubo é submetido a um torque de 750 N · m. Determine a parcela desse torque à qual a seção sombreada cinza resiste. Resolva o problema de duas maneiras: (a) usando a fórmula da torção e (b) determinando a resultante da distribuição da tensão de cisalhamento.

Passo 1

Neste problema, sabendo que o tubo é submetido a um torque de 750 N.m, precisamos determinar a parcela desse torque à qual a seção sombreada cinza resiste, certo?

Só que temos um “porém”. Para determinarmos essa parcela, devemos primeiro usar a fórmula da torção e depois determinando a resultante da distribuição da tensão de cisalhamento.

Parece muita coisa, mas é bem tranquilo. Para resolver o item (a) do exercício, utilizaremos a fórmula de torção:

τ m á x = T × c J

Já para o item (b), utilizaremos as expressões a seguir:

d T = ρ × σ × d a

d a = 2 × π × ρ d ρ

Então, vamos lá?

Passo 2

Como já sabemos para o item (a), utilizaremos a seguinte fórmula:

τ m á x = T × c J

Sendo J o nosso momento polar de inércia, que é dado por:

J = π 2 × c 4

Peguem a visão, se temos um tubo com diâmetros externo e interno ele é oco! Em outras palavras ele é vazado, e isso vai interferir diretamente no cálculo de J.

J = π 2 0,1 4 - 0,025 4 = 1,56 × 10 - 4 m 4

Vamos atribuir valores à fórmula de torção para determinar a tensão na seção:

τ m á x = 750 N . m × 0,1 m 1,56 × 10 - 4 m = 479337,24 N m 2 = 0,479 M P a  

Passo 3

Agora que encontramos o valor da tensão máxima na seção, vamos descobrir o valor da parcela desse torque à qual a seção sombreada cinza resiste, ou seja, o valor que esta parcela causa em c i = 75 m m :

τ = T ' × c 0 π 2 c 0 4 - c i ' 4

Substituindo os valores a gente tem:

0,479 × 10 6 N m 2 = T ' × 0,1 π 2 0,1 4 - 0,075 4

E aí nos dá ao isolar T’:

T ' = 0,479 × 10 6 × π × 0,1 4 - 0,075 4 2 × 0,1 = 514,34   N . m

Passo 4

Como já foi dito lá no passo 1, para resolver o item (b), utilizaremos as expressões a seguir:

d T = ρ × τ × d a

d a = 2 × π × ρ d ρ

A primeira expressão é utilizada para encontrar o torque em um trecho de área d a . A área d a é o perímetro vezes a espessura da região em estudo.

Para desenvolver a fórmula d T , devemos substituir o valor da tensão ( τ ) pela equação abaixo:

τ = ρ c × τ m á x

Por fim, substituindo os valores na fórmula d T :

d T ' = ρ × ρ c × τ m á x × 2 × π ρ d ρ = 2 π τ m á x c ρ 3

E integrando para os limites do raio onde:

0,075 m < ρ < 0,1 m

Temos:

∫ 0 T ' d T ' = 2 π τ m á x c ∫ 0,075 0,1 ρ 3 d ρ

T ' = 2 π τ m á x c × ρ 4 4 0,075 0,1

E substituindo nos dá:

T ' = 2 π × 0,479 × 10 6 0,1 × 0,1 4 - 0,075 4 4

T ' = 514,34   N . m

Resposta

  1. T = 514,34   N . m
  2. T ' = 514,34   N . m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O eixo maciço de alumínio tem diâmetro de 50mm . Determine a tensão de cisalhamento máxima absoluta no eixo e trace um rascunho da distribuição da tensão de cisalhamento ao longo da linha radial do ei
O eixo maciço com 60mm de diâmetro está sujeito aos carregamentos de torção distribuídos e concentrados mostrados na figura. Determine a tensão de cisalhamento nos pontos A e B e trace um rascunho da
Um eixo é feito de uma liga de aço com tensão de cisalhamento admissível τ a d m = 84MPa . Se o diâmetro do eixo for 37,5mm , determine o torque máximo T que pode ser transmitido. Qual seria o torque
O eixo tem diâmetro externo de 32mm e diâmetro interno de 25mm . Se for submetido aos torques mostrados na figura, faça o gráfico da distribuição de tensão de cisalhamento que age ao longo de uma linh
O eixo maciço de alumínio tem diâmetro de 50mm e tensão de cisalhamento admissível τ a d m = 6MPa . Determine o maior torque T 1 que pode ser aplicado ao eixo se ele também estiver sujeito a outros ca