Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 6.Problemas - Ex. 108
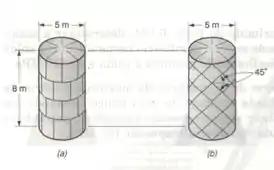
Placas quadradas, cada uma com de espessura, podem ser soldadas juntas de dois modos distintos, como mostrado, para formar um tanque cilíndrico de ar comprimido. Sabendo-se que a tensão normal admissível perpendicular à solda é , determinar a maior pressão admissível em cada caso.
Passo 1
Fala ai galera, agora vamos para uma questão que vamos usar dois conceitos muito legais que aprendemos. Um desses conceitos é o cálculo das tensões principais que sabemos que devemos usar as fórmulas abaixo para o caso de estruturas cilíndricas.
- Sabemos que a nossa tubulação é cilíndrica e não esférica, nesse caso, usaríamos as seguintes equações:
- Sabemos que o nosso diâmetro dado, é o diâmetro externo, ou seja, precisamos descontar a espessura, sendo assim temos que:
- E sabemos que é a espessura
- é a pressão que age na nossa estrutura
Até aqui tudo certo, certo? Mas ai entra uma coisa bem legal, lembra que agora queremos as tensões que agem na nossa solda, que está girada de um ângulo com relação ao estado plano de tensões principais.
Agora pensa comigo, sempre que eu tenho um estado plano de tensões, e giro esse estado plano de tensões, qual a nova fórmula que eu uso para isso???? EXATAMENTE as nossas três formulazinhas que usamos quando queremos girar a nossa seção, com isso teremos que:
Agora sim temos toda a matéria prima para resolver o nosso problema, vamos nessa??
Passo 2
Sabemos pelo enunciado que:
Calculando o raio, temos que:
Calculando a tensão, teremos que:
Agora veja o seguinte, no caso a) a nossa seção não está girada, ou seja, as tensões atuantes, já são as tensões atuais calculadas, ou seja, já podemos determinar qual a máxima pressão que age no caso a) considerando que a tensão perpendicular a face de ligação é a maior das duas calculadas acima, lembrando que como calculamos o estado de tensões principais, não temos tensões cisalhantes agindo, sendo assim, temos que:
E assim resolvemos metade do nosso problema, agora vamos girar a nossa seção para encontrarmos as tensões na nossa solda a . Fica tranquilo que já estamos no finalzinho, vamos dar um último gás.
Passo 3
Sabemos que:
Substituindo teremos que:
Começaremos com a tensão em x.
Vamos para a próxima tensão.
Agora vamos para a tensão em y.
Olhando o nosso elemento girado, temos que:
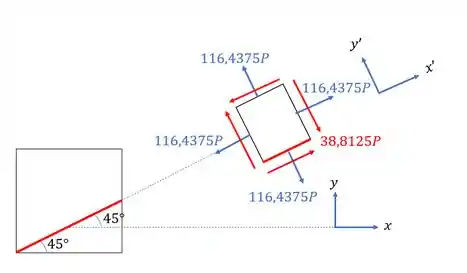
Assim temos que:
- Tensão normal perpendicular ao filete é dada pela .
E pensa no seguinte, temos que a tensão admissível dada para o caso de esforço normal perpendicular a seção da solda é dada por , igualando as duas tensões tem-se que: