Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 13.Problemas - Ex. 17

17. Resolva o Problema 13.16, se a coluna estiver presa por pinos no topo e na base.

Passo 1

Bem! Como a coluna está presa por pinos no topo e na base, de cara já tiramos que o seu fator de comprimento efetivo K é igual a 1 .

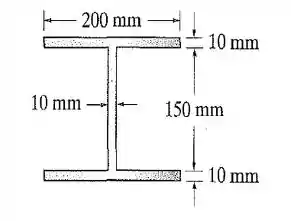
Agora, vamos tratar de obter o momentos de inércia em relação ao eixo y do nosso sistema.

I y = 2 × 1 12 b 1 h 1 3 + 1 12 b 2 h 2 3

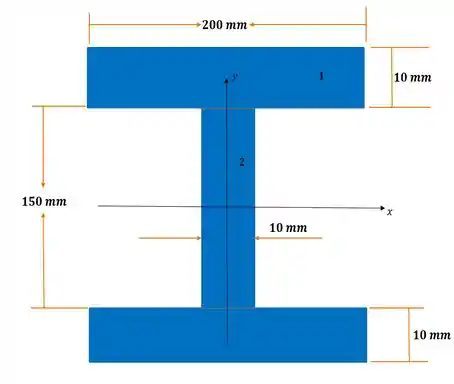
Onde:

b 1 = 10   m m

h 1 = 200   m m

b 2 = 10   m m

h 2 = 150   m m

Logo, chegamos ao seguinte resutado:

I y = 2 × 1 12 ( 10   m m ) 200   m m 3 + 1 12 ( 10   m m ) ( 150   m m ) 3

I y ≅ 13345833,333   m m 4 ≅ 13,346 ⋅ 10 - 6   m 4

Pronto! Já sabemos o momento de inércia I y em relação ao eixo y .

Passo 2

Vamos então, usar a fórmula da carga crítica para a flambagem:

P c r = π 2 E I y ( K L ) 2

E substituindo os valores numéricos pertencentes a cada variável, chegamos até:

P c r = π 2 ( 200 ⋅ 10 9   P a ) ( 36,6 ⋅ 10 - 6   m 4 ) ( 1 ⋅ 9,0   m ) 2

P c r ≅ 325229,86   N     ≅ 325,23   k N

Agora, que já achamos sabemos o valor da carga crítica P c r , apliquemos então a outra velha e conhecida fórmula de tensão, dada pela divisão da força P c r pela área A em que ela atua:

σ c r = P c r A

σ c r = 325229,86     N 2 200   m m ⋅ 10   m m + ( 150   m m ⋅ 10   m m )

σ c r =   325229,86   N 5,5 ⋅ 10 - 3   m 2

σ c r ≅ 59,13   M P a

Esse valor é menor do que a tensão admissível para o nosso aço, que é igual a 250   M P a . Logo, está tudo certo com o resultado!

Resposta

C a r g a   c r í t i c a → P c r ≅ 325229,86   N     ≅ 325,23   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O elemento estrutural feito de liga de alumínio 2014-T6 tem seção transversal simétrica. Se estiver acoplado por pinos nas extremidades, determine a maior força que ele pose suportar.
A coluna de aço tem comprimento de 5 m e é livre no topo e engastada na base. Se a área da seção transversal tiver as dimensões mostradas na figura, determine a carga crítica. e = 200 G P a e σ y = 36
Considere que as extremidades da barra de aço A B da estrutura estejam acopladas por pinos para flambagem no eixo y - y . Se P=18k N , determine o fator de segurança para flambagem em torno do eixo y
Determine a carga máxima P que a estrutura pode suportar sem provocar flambagem no elemento estrutural A B . Considere que AB é feito de aço e que suas extremidades estão presas por pinos para flambag
O mecanismo articulado é composto por duas hastes de aço A-36, cada uma com seção transversal circular. Determine, com aproximação de múltiplos de 5 mm, o diâmetro de cada haste que suportará uma carg