Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 9.Problemas - Ex. 46
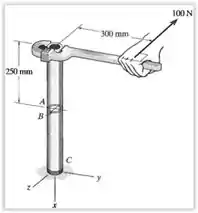
46. O tubo de aço tem diâmetro interno de e diâmetro externo de Se estiver preso em e for submetido à força horizontal de que age na extremidade do cabo da chave, determine as tensões principais no tubo no ponto localizado na superfície do tubo.
Passo 1
Fala galerinha do RespondeAí, tudo jóia?
Saca só, esse exercício aqui fala pra gente que o tubo de aço em um diâmetro interno de e um diâmetro externo de , dado que ele está preso em , o enunciado nos diz que se ele for submetido à força horizontal de que age na extremidade do cabo, então é pra gente determinar as tensões principais no ponto localizado na superfície do tubo.
Então belezoca, primeiro, vamos montar o diagrama de forças e momentos atuantes no tubo:
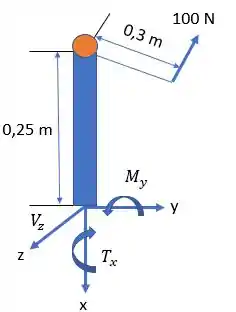
Agora, é só fazer a análise de esforços atuantes no ponto , que é o ponto onde queremos achar as tensões principais:
Então para o momento em , obtemos:
Do mesmo modo, para o momento em :
Passo 2
Agora, é só acharmos a tensão máxima de cisalhamento no Ponto pela fórmula a seguir, lembrando que a fórmula do momento polar de inércia de um círculo é da por , onde é a distância do centro até a bora mais externa:
Onde é a distância do centro do tubo até o ponto , ou seja, a parte mais externa do tubo:
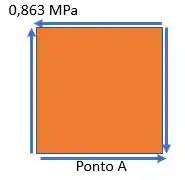
Passo 3
Agora, é só achar as tensões principais no ponto :
Essa fórmula nos fornece duas tensões, uma máxima e outra mínima :
Segue que:
Resposta
As tensões principais no ponto são: