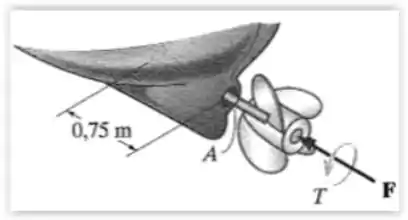
44. O eixo maciço da hélice de um navio estende-se para fora do casco. Em operação, ele gira a quando o motor desenvolve de potência, o que causa um impulso de no eixo. Se o diâmetro externo do eixo for , determine as tensões principais em qualquer ponto localizado na superfície do eixo.
Passo 1
E aí meu aprovado!! Aqui vamos nós de novo pra mais uma questãozinha de ResMat.
Olha só, não deixa essa situação toda do barco, hélice, casco e tudo mais te assustar. Basicamente, temos um eixo, que sofre uma potência que gera um torque. Então ele vai sofrer tensão de cisalhamento por causa dele.
E esse eixo também sofre uma força normal . Pelo equilíbrio, essa força precisa aparecer do outro lado do eixo. Juntas, essas duas bonitas causam compressão. Mais uma tensão aí!
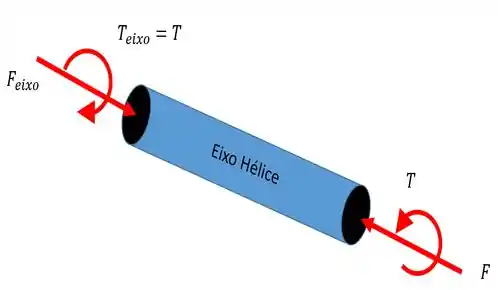
A ideia é a gente calcular essas tensões para essa situação e depois achar as tensões principais, como o enunciado pede. Vamos!
Passo 2
Já sabemos que a força é a força do impulso causado pelo motor e é força de reação do eixo pra compensar ... Elas tem o mesmo módulo.
A mesma coisa acontece pro torque. O torque do eixo é igual ao torque do motor ...
Sendo assim, como o exercício deu a velocidade angular e a potência que o motor desenvolve, a gente pode achar o que quer pela fórmula abaixo:
Molezinha, né!? Potência é igual ao produto da velocidade angular pelo torque...
Substituindo os dados do enunciado, obtemos então, que o nosso torque é de:
Tal que:
E consequentemente:
Passo 3
Agora, vamos trabalhar pra achar as tensões nessa situação
Para isso, bora seguir o procedimento padrão que a gente sempre está acostumou a fazer...
Primeiro, bora obter a tensão normal, que no nosso caso, é dada por
Bem! A força normal no eixo, é a força , de compressão, porque está aplicada em um sentido que tende a encurtar a peça.
E se ela é de compressão, então seu sinal é negativo, igual a . Quanto à área da seção transversal do eixo, é molezinha. Trata-se basicamente da área de um círculo, que já estamos cansados de saber.
Substituindo assim, os valores numéricos, obtemos que:
Passo 4
A próxima coisa a se fazer agora, é obter a tensão de cisalhamento no eixo. Pois muito bem! Podemos fazer isso através da expressão abaixo:
Lembrando que o momento polar de inércia da seção transversal de um sólido com seção circular cheia, que é o caso do nosso eixo, é dado pela seguinte fórmula:
Onde é o raio da nossa seção, igual à:
Já a variável . Bem! Ela é a distância do centro do eixo até o ponto que está sendo estudado, que é qualquer ponto na superfície do eixo.
Mas qual ponto, vamos pegar?
Pergunta difícil, hein parceiro(a)?
Sla! Bora pegar o ponto mais distante possível do centro do eixo... De acordo com a figura abaixo:
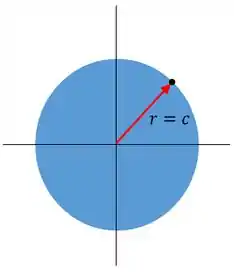
E conforme podemos ver, esse ponto está a uma distância do centro do eixo.
Aí sim! As coisas agora, estão bem mais claras.
Já não temos mais o que fazer! Como já descobrimos tudo que faltava, bora voltar à fórmula da tensão cisalhante...
Onde substituindo os valores numéricos de cada variável:
Passo 5
E aqui está um esboço dessas tensões, representadas em um elemento plano; pra deixar ainda mais claro nosso entendimento.
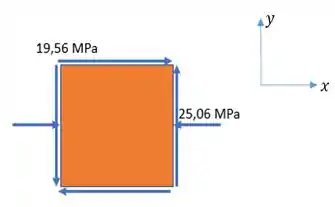
A imagem acima corresponde ao estado plano de tensões...
Dela... tiramos os seguintes dados:
Passo 6
E pra finalizar, bora obter as tensões principais no eixo...
Pra isso já sabe, né!? Temos que recorrer à seguinte fórmula abaixo...
Onde trocando as variáveis pelos seus valores conhecidos anteriormente:
Podemos obter duas tensões. A primeira vai ser a tensão máxima, que é igual à:
E a outra vai ser a tensão mínima, que vale:
Resposta
Tensões principais no eixo: