Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 18
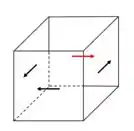
O tubo de cobre tem diâmetro externo de e diâmetro interno de . Se estiver firmemente preso à parede em e for submetido a um torque uniformemente distribuído, como mostra a figura, determine a tensão de cisalhamento desenvolvida nos pontos e . Esses pontos se encontram na superfície externa do tubo. Faça um rascunho da tensão de cisalhamento sobre os elementos de volume localizados em e .
Passo 1
Um tubo sofre um carregamento de torção uniformemente distribuído: .
Queremos achar a tensão de cisalhamento em dois pontos: e .
Sabemos que a fórmula da torção para cisalhamento é
Características do eixo:
- Raio interno: .
- Raio externo: .
- Momento polar de inércia: .
O é constante pro eixo todo. Os pontos e estão na borda do eixo (então usamos . O que nos falta saber é a torção e nas seções transversais em e !
Depois disso, a questão pede que desenhos a tensão em um elemento de volume (um cubinho!) onde esses pontos estão.
Passo 2
Precisamos descobrir qual é o torque acontecendo em cada parte do eixo. Isso é tranquilo!
Primeiro, escolha um sentido do torque pra ser positivo. Vamos escolher o sentido a para isso. Aponte seu dedão direito nesse sentido. Se o torque seguir seus dedos quando fecham, é positivo. Se não seguir, negativo
Aí quebre o eixo em seções. Vamos por partes, calculando o torque.
- Torque na seção a partir da extremidade livre até :
- Torque na seção da extremidade livre até :
Passo 3
Agora que temos os torques, vamos usar a fórmula para achar a tensão.
Primeiro a tensão no ponto :
Agora a tensão em :
Beleza, mas e os sinais? Essas tensões estão apontando pra onde? Tudo depende de como você corta a seção! Vamos ver!
Passo 4
Vamos olhar uma seção que vai da extremidade livre até a seção transversal em .
Seguindo a nossa convenção (Passo 2), temos aplicado na extremidade livre, e aí o torque interno em tem que ser para equilibrar! Negativo!
Se é negativo, aponte seu dedão para e feche os dedos. Veja o sentido que seus dedos apontam para como o ponto está no eixo! Vai ser a seta vermelha na figura.
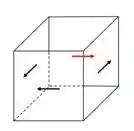
A face onde está a seta vermelha é a face mais externa para o ponto segundo a seção que estamos imaginando! Para achar o sentido das outras setas é fácil, só pensar no equilíbrio em cada direção!
Passo 5
Agora vamos ver uma seção que vai da extremidade livre até a seção transversal em .
Seguindo a nossa convenção (Passo 2), temos aplicado na extremidade livre, então o torque interno em tem que ser para equilibrar! Negativo!
Se é negativo, aponte seu dedão para e feche os dedos. Veja o sentido que seus dedos apontam para como o ponto está no eixo! Vai ser a seta vermelha na figura.
A face onde está a seta vermelha é a face mais externa para o ponto segundo a seção que estamos imaginando! Para achar o sentido das outras setas é fácil, só pensar no equilíbrio em cada direção!
Resposta
Tensão em : .
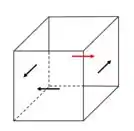
Tensão em : .
