Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 10.Problemas - Ex. 30
A roseta de deformação a 45° está montada próxima ao dente da ferramenta. As seguintes leituras foram obtidas para cada extensômero: ;e Determine (a) as deformações principais no plano e (b) a deformação por cisalhamento máxima no plano e a deformação normal média. Em cada caso, mostre o
elemento distorcido devido a essas deformações.
Passo 1
a) Fala galera, bora pra mais um problema de Resmat? Boraaa!
O problema quer que a gente determine as deformações principais no plano.
Vamos colocar o eixo positivo na direção e sentido de . Aí nessa direção a gente tem e cresce no sentido anti-horário. E assim positivo aponta na direção de .
Então temos que as deformações nos extensômetros e as orientações deles são:
A ideia é achar as deformações normais e de cisalhamento no plano . E através delas achar as deformações principais. Vamos lá!
Passo 2
Com esse sistema de referências que a gente escolheu, podemos achar as deformações nos nossos eixos. No eixo vamos ter:
Para o eixo :
E por essa fórmulinha aqui a gente acha a deformação de cisalhamento no plano:
Substituindo os nossos dados e calculando:
Aí com isso a gente consegue achar as principais. Vem!
Passo 3
Para calcularmos as deformações principais vamos usar a seguinte fórmula:
Sendo que
Subsituindo, ficamos com:
E para
Passo 4
A orientação do elemento será dada por:
Vamos dizer que essa é a orientação do nosso eixo . Para saber qual a tensão principal relacionada a esse eixo, a gente usa:
Substituindo nossos valores:
Reapara que essa é que a gente achou. Então a deformação em vai ser
Obs: o gabarito diz que o ângulo é diferente, mas pela fórmulinha para descobrir quem era , vemos que nosso ângulo está certo porque achamos , tudo bem? Então estamos certinhos!
Passo 5
Aí fazendo o desenho do elemento na orientação onde temos as tensões principais:
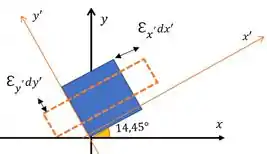
Percebe que como é negativo a deformação que ele causa no elemento reduz sua altura em .
Passo 6
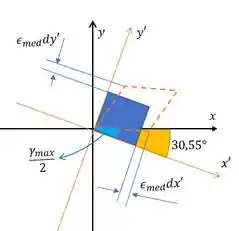
b) Na letra b, ele nos pede a deformação por cisalhamento máxima e a deformação média associada. A deformação de cisalhamento máximo é dada pela fórmulinha:
E a deformação normal média associada é a média das nossas deformações:
Passo 7
Já a orientação, será dada por:
Substituindo e calculando
E aí a gente usa esse ângulo para saber o sinal certo da deformação de cisalhamento pela fórmulinha:
Substituindo nossos dados aí e isolando
Ele é positivo mesmo como a gente achou antes. Aí pela convenção essa distorção faz com que o ângulo reto do elemento que tem vértice na origem diminua.
Obs: por essa fórmula de verificação, vemos também que o ângulo que achamos está certinho. E que o gabarito pode estar com um errinho mesmo, tá?
Passo 8
Nosso elemento bonito para essa situação fica assim:
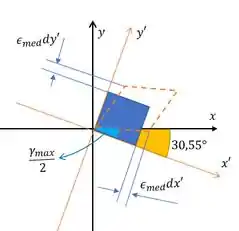
Resposta
a)
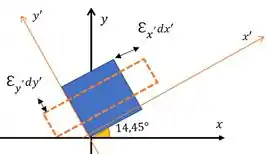
b)
