Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 3.Problemas Revisão - Ex. 138b
O arranjo mostrado de eixos com polias para correias planas é usado para transmitir 2 kW do ponto A para o ponto D. Pede-se (a) usando uma tensão de cisalhamento média de 70 Mpa, determinar a velocidade de rotação adequada para o eixo AB (b) resolver a parte , assumindo que os diâmetros dos eixos AB e CD são 18 mm e 15 mm, respectivamente.
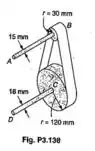
Passo 1
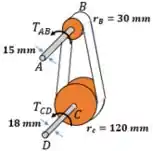
A relação de transmissão por correias é dada pelo raio das polias. Então a razão de transmissão é:
Com a razão de transmissão podemos relacionar os torques:
Passo 2
Pronto, agora vamos calcular o torque admissível em cada eixo. Podemos fazer isso lembrando que a tensão em um eixo sobre torção é dada por:
Como o eixo é circular maciço, podemos aplicar que:
Simplificando:
E assim, isolamos o torque em função do raio .
E para descobrir o torque admissível em cada eixo, basta a gente aplicar o valor da tensão admissível e o valor do raio . Para o eixo AB
Para o eixo CD
Passo 3
Agora vamos testar as duas possibilidades para descobrir a maior tensão admissível.
Se :
Neste caso o torque em CD supera o torque admissível. Então essa não é uma alternativa possível.
Mas no caso de :
Essa é uma alternativa possível.
Passo 4
Agora que conhecemos o torque em podemos calcular a sua velocidade, utilizando a equação da potência:
Para converter para multiplicamos por