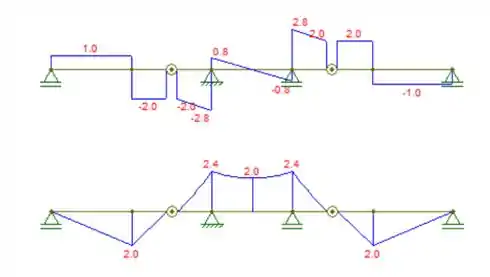
Represente graficamente os diagramas de força cortante e momento fletor para a viga composta. Os três segmentos estão interligados por pinos em e .

Passo 1
Fala galerinha bonita, show de bola com vocês?
Saca só, nesse exercício aqui o enunciado nos pede para representar graficamente os diagramas de força cortante e momento fletor para a viga composta.
Belezoca, sendo assim s viga deve ser estudada por partes. Para isso, faremos o somatório em B (rótula), considerando apenas seu lado esquerdo:
Como temo suma relação de simetria entre e podemos tirar que:
Iradoso, agora podemos também fazer o somatório em C, tal que:
Sendo assim, obtemos que:
Mais uma vez, por simetria conseguimos obter que:
Maravilha, agora que a gente tem os valores das reações na viga, vamos determinar as equações dos esforços internos. Bora lá!
Passo 2
Show de bolinhas, pra gente escrever as equações de esforços internos vamos precisar dividir a viga em seções, sendo assim vamos obter que:
Seção 1, contida no intervalo :
Obtemos que o momento será:
E como temos a relação:
Tiramos que:

Passo 3
Maravilha, agora vamos pra próxima seção:
Seção 2, contida no intervalo :
Obtemos que:
Logo:
Agora para a Seção 3 contida no intervalo , obtemos que:
Seção 4, contida no intervalo , vamos obter:
Seção 5, contida no intervalo :
Seção 6, no intervalo :
E por fim, na Seção 7 do intervalo , vamos obter que:
Passo 4
Portanto, as equações dos esforços internos serão dadas como:
Como temos todas as forças e momentos calculados, podemos desenhar os diagramas de cortante e fletor, respectivamente, tomando-se o cuidado de que o momento nas rótulas é nulo. Logo:
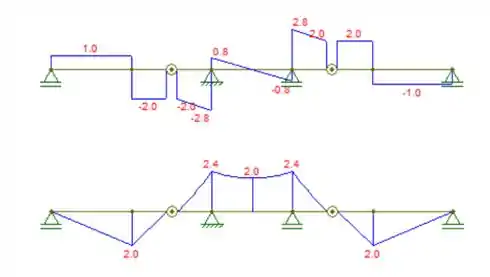
Resposta