Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 6.Problemas de Revisão - Ex. 99

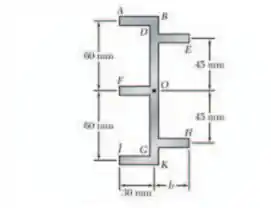
Uma viga de paredes finas com espessuras uniforme tem a seção transversal mostrada. Determine a dimensão b de modo que o centro de cisalhamento O da seção transversal fique localizado no ponto indicado.

Passo 1

E ai galera tudo bem??? O enunciado pede que a gente determine a dimensão b de modo que o centro de cisalhamento O da seção transversal fique localizado no ponto indicado, então vamos dividir por seções para facilitar!

Parte AB

A = t x y - = 60   m m

Q =   A y - =   60 t x   m m 3

τ = V Q I t = 60 V x I

F 1 = ∫ τ d A = ∫ 0 30 60 V x I t   d x = 60 V t I ∫ 0 30 x d x = 60 V t I x 2 2 0 30 = 60 30 2 2 V t I = 27 × 10 3 V t I

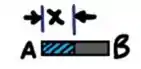
Passo 2

Parte DE:

A = t x y - = 45   m m

Q = A y - = 45 t x

τ = V Q I t = 45 V x I

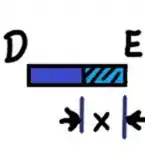
Considerando o esboço abaixo temos:

F 2 =   ∫ τ   d A =   ∫ O b 45 V x I t   d x   = 45 V x I ∫ O b x   d x =   45 b 2 V t 2 I

+ ↶ Σ M O = + ↶ Σ M O : 0 = 2 45 F 2 - 2 60 F 1

45 2 b 2 - 2 60 27 × 10 3 V t I = 0

b 2 = 2 60 27 × 10 3 45 2 = 1600   m m 2 = b = 40   m m

Resposta

40   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere o caso geral de uma viga prismática sujeita às componentes de momento fletor Mye Mz, como mostra a figura, quando os eixos x, y, z passam pelo centroide da seção transversal. Se o material f
Três placas de aço de 120m m × 10m m foram soldadas para formar a viga mostrada na figura. Considerando que o aço seja elastoplástico com E = 200G P a e σ E = 300M P a , determine ( a ) o momento flet
As quatro forças mostradas na figura abaixo são aplicadas a uma placa rígida suportada por um poste de aço cheio de raio a . Sabendo que P = 100k N e a = 40m m , determine a tensão máxima no poste qua
Três pranchas de madeira são conectadas com parafusos de 14 mm de diâmetro espaçados a cada 150 mm ao longo do eixo longitudinal da viga. Para uma força cortante vertical de 10 kN, determine a tensão
Uma viga com a seção transversal mostrada na figura está submetida a um momento M 0 que atua em um plano vertical. Determine o maior valor admissível do momento M 0 se a tensão máxima na viga não deve