Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 6.Problemas de Revisão - Ex. 100

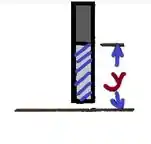
Determine a localização do centro de cisalhamento O de viga de paredes finas de espessuras constante que possui a seção transversal mostrada.

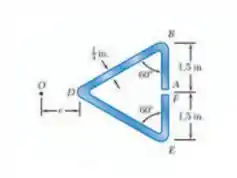
Passo 1

Então pessoal prontos pra mais uma ?!? Vamos começar calculando de maneira fracionada por trechos, antes considere nosso esboço a seguir :D

Passo 2

Vamos começar calculando a inercia dos trechos, vem comigo :D

I A B = 1 3 1 4 1,5 3 = 0,28125   i n 4

L B D = 3   i n A B D = 3 1 4 = 0,75   i n 2

I B D = 1 3 A B D h 2 = 1 3 0,75 1,5 2 = 0,5625   i n 4

E a inércia total é:

I = 2 0,28125 + 2 0,5625 = 1,6875   i n 4

Passo 3

Considere as informações a seguir:

A = 1 4 y y - = 1 2 y Q = A y - = 1 8 y 2

τ = V Q I t = V y 2 8 1,6875 0,25 = V y 2 3,375

F 1 =   ∫ τ d A = ∫ 0 1,5 V y 2 3,375 0,25 d y = 0,25 V 3,375 y 3 3 0 1,5 = 0,25 1,5 3 3,375 3 = 0,083333 V

+ ↶ M D = + ↶ M D : V e = 2 F 1 3   s i n   60 °

V e =   ( 2 ) ( 0,083333 ) V 3   s i n   60 °

e =   ( 2 ) ( 0,083333 ) 3   s i n   60 ° =   0,433   i n

Resposta

0,433   i n

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a viga de mesas largas com o carregamento mostrado, determine a maior carga P que pode ser aplicada, sabendo-se que a tensão normal máxima é de 24 ksi e a maior tensão de cisalhamento usando a ap
Para a viga e o carregamento mostrado, considere a seção n-n e determinar (a) a maior tensão de cisalhamento em nessa seção, (b) a tensão de cisalhamento no ponto a.
Determine a tensão máxima em cada um dos elementos de máquina mostrados.
A parte curva da barra mostrada na figura tem um raio interno de 20m m . Sabendo que a tensão admissível na barra é de 150M P a , determine a maior distância possível da linha de ação da força de 3k N
A parte vertical da prensa mostrada na figura consiste em um tubo retangular com espessura de parede t = 10m m . Sabendo que a prensa foi usada para prender blocos de madeira que estavam sendo colados