Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 6.Problemas de Revisão - Ex. 97

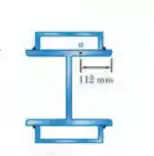
A viga composta mostrada é feita soldando perfis U laminados de aço C 200   x   17,1 as mesas do perfil de aço laminados de mesas largas W   250   x   80 . Sabendo que a viga é submetida a uma força cortante de 200   k N ,determine a a força cortante horizontal por metro em cada solda, b a tensão de cisalhamento no ponto a da mesa do perfil de mesas largas.

Passo 1

E ai gurizada tudo belezinha? O enunciado pede que a gente determine a força cortante horizontal por metro em cada solda e a tensão de cisalhamento no ponto a da mesa do perfil de mesas largas. Então considere o esboço abaixo :D

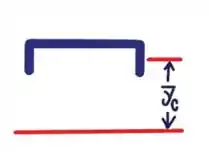
Considere os dados abaixo:

Para W 250 × 80 , d = 257   m m , t f = 15,6   m m , I x = 126 × 10 6 m m 4

Para C 200 × 17,1 , d = 2170   m m 2 , b f = 57,4   m m , t f = 9,91   m m

I y = 0,545 × 10 6 m m 4 , x _ = 14,5   m m

Passo 2

Para o canal na viga composta,

y c _ = 257 2 + 57,4 - 14,5 = 171,4   m m

Para a viga composta,

I = 126 × 10 6 + 2 0,545 × 10 6 + 2170 171,4 2 = 254,59 × 10 6 m m 4 = 254,59 × 10 - 6 m 4

(a) para as duas soldas,

Q w = A y c _ = 2170 171,4 = 371,94 × 10 - 6 m m 3 q = V Q I = 200 × 10 3 371,94 × 10 - 6 254,59 × 10 - 6 = 292,2 × 10 3 N / m

Para uma solda,

q 2 = 146,1 × 10 3   N / m

Força de cisalhamento por metro de solda: 146,1   k N / m

Passo 3

(b) Para cortes em ‘a’ e 'a’ juntos, considere o esboço abaixo :D

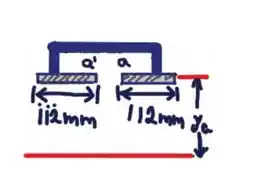
A área é dada por:

A a = 2 112 15,6 = 3494,4   m m 2

y a _ = 257 2 - 15,6 2 = 120,7   m m

Q a = 371,94 × 10 3 + 3494,4 120,7 = 793,71 × 10 3 m m 3 = 793,71 × 10 - 6 m 3

Uma vez que temos cortes ‘a’ e ‘a ' em, t = 2 t f = 2 15,6 = 31,2   m m   =   0,0312   m

τ a = V Q a I t = 200 × 10 3 793,71 × 10 - 6 254,59 × 10 6 0,0312 =   19,99 × 10 6 P a = 19,99   M P a

Resposta

  1. 146,1 k N m
  2. 19,99   M P a
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A tábua é usada como uma trave de assoalho simplesmente apoiada. Se um momento fletor M = 1,2 kN.m for aplicado a 3º em relação ao eixo z, determine a tensão desenvolvida na tábua no canto A. Compare
O eixo de 30 mm de diâmetro está sujeito às cargas verticais e horizontal de duas polias como mostra a figura. O eixo está apoiado em dois mancais em A e B, que não oferecem nenhuma resistência à carg
O eixo está sujeito às cargas vertical e horizontal de duas polias, como mostra a figura, e está apoiado em dois mancais em A e B, que não oferecem nenhuma resistência à carga axial. Além do mais, pod
Usando as técnicas descritas no Apêndice A, Exemplo A.5 ou A.6, a seção em Z tem momentos principais de inércia Iy= 0,060(10-3)m4 e Iz= 0,471(10-3)m4, calculados em torno dos eixos principais de inérc
O eixo de aço de 65 mm de diâmetro está sujeito a duas cargas que agem nas direções mostradas na figura. Se os mancais em A e B não exercerem uma força axial sobre o eixo, determine a tensão de flexão