Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 34
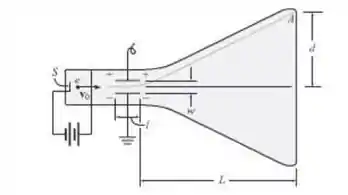
No tubo de raios catódicos, elétrons tendo massa m são emitidos de um ponto-fonte S e começam a se mover horizontalmente com uma velocidade inicial . Quando passam entre as placas-grade em uma distância l, eles são sujeitos a uma força vertical tendo uma intensidade , onde é a carga de um elétron, é a voltagem aplicada atuando através das placas, e é a distância entre as placas. Após passarem as placas, os elétrons então se movem em linha reta e atingem a tela em A. Determine a deflexão dos elétrons em termos das dimensões da placa de voltagem e do tubo. Despreze a gravidade que causa uma ligeira deflexão vertical quando o elétron se move de S até a tela, e a ligeira deflexão entre as placas.
Passo 1
Este problema é bem semelhante com aqueles de lançamentos inclinados vistos no capítulo 12. Neles, uma partícula possuía velocidade constante no eixo e estava sujeito a gravidade no eixo . Aqui, o elétron está sujeito a uma força no eixo , e possui velocidade constante no eixo .
Para resolvermos, precisamos determinar o tempo necessário para ele percorrer a distância L. Depois, vamos analisar o efeito desta força vertical, a qual é capaz de causar uma deflexão d.
Passo 2
Nosso primeiro passo é calcular o tempo necessário para que o elétron passe pela região em que ele é submetido a uma força e o tempo necessário para que atinja a tela em A. Começando pelo tempo , temos:
Já para o tempo , teremos:
Passo 3
Agora que já descobrimos o tempo, vamos calcular o valor da aceleração do elétron. Portanto, temos:
Após a passagem do tempo , a sua velocidade será:
Passo 4
Após o elétron passar entre as duas placas de comprimento , ele não estará sujeito mais a ação de forças. Portanto, sua velocidade será constante. Desta forma, o comprimento percorrido será: