Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 48
O bloco B de e o cilindro A de estão ligados por uma corda leve que passa por um buraco no centro da mesa lisa. Se ao bloco é dada uma velocidade circular de , determine o raio da trajetória circular ao longo da qual ele se move.
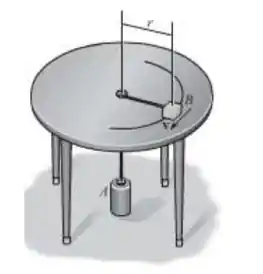
Passo 1
Temos um problema de cinética que envolve rotação. Devido a configuração do problema o bloco B, que possui uma velocidade constante igual a , possui apenas uma componente normal da aceleração a sua trajetória, representada pela tração na corda. E esta mesma tração é igual ao peso do bloco A, pois este se encontra em equilíbrio estático.
Precisamos então aliar as equações da cinética com cinemática para podermos calcular o raio de rotação do bloco B.
Passo 2
Vamos começar determinando a tração na corda. Como o bloco A encontra-se em equilíbrio estático, temos então:
Passo 3
Agora que descobrimos a tração na corda e, consequentemente, a força centrípeta do bloco A, podemos calcular o valor da componente normal da sua aceleração. Portanto, temos:
Lembrando a equação da aceleração normal lá da cinemática, temos: