Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 11.Problemas - Ex. 76a
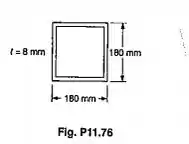
Um tubo de com a a seção transversal mostrada e é usado como uma coluna, sabendo-se que =320MPa e E=200GPa, determinar a carga centrada admissível, se o comprimento efetivo da coluna é de:(a) 9,6m;(b)7,2m.
Passo 1
Fala meus projetistas bora pra mais uma?
Vamos á um problema de projeto, aqui não tem muito mistério pra encontrar a carga centrada a gente precisa calcular a geometria, avaliar para qual intervalo de esbeltez se encontra a nossa coluna e aplicar para o intervalo as equações corretas. Vamos então nos atentar aos limites, nosso índice de esbeltez é dado por:
Onde:
é o comprimento efetivo, e é o raio de giração dado por:
Vamos calcular o parâmetro e avaliar alguns limites para , esse parâmetro é dado por:
E aí temos 2 condições.
Se estiver acima do mostrado, a coluna não pode ser projetada, vamos focar em encontrar onde o nosso parâmetro se encontra e aí para cada caso traremos a formulação necessária pra encontrar a tensão admissível e depois relacionar com da seguinte forma:
Passo 2
Como a seção é quadrada vazada não há eixo fraco como podemos ver na figura:
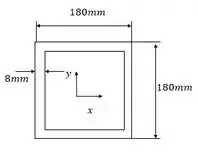
e o momento de inércia pode ser dado por:
E substituindo:
E para o raio de giração também precisamos da área que é dada por:
E aí:
Enfim temos:
Passo 3
Vamos então ao nosso índice de esbeltez, e para o item a. o comprimento efetivo é 9,2m ou 9200mm.
E o nosso parâmetro :
Ou seja:
Daí para esse tipo de condição a tensão admissível é dada por:
E substituindo:
E como:
Temos:
E em :