Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 3.Problemas - Ex. 23
Um tubo está sendo dobrado pelo dobrador de tubos, conforme mostrado. Se o cilindro hidráulico aplica uma força de magnitude ao tubo em , determine a magnitude das reações do rolo em e .
Passo 1
Fala galera! Tudo certo? Vamos dividir a resolução em algumas etapas, beleza? Prometo que vai ser bem rapidinho!
O enunciado nos pede para determinar o módulo das reações nos pontos e devido à aplicação de uma força . Vamos começar fazendo o diagrama de corpo livre do nosso sistema de forças. Isolando o tubo com as três forças que estão agindo nele, temos: as duas reações e dos apoios e a força exercida pelo cilindro no ponto .
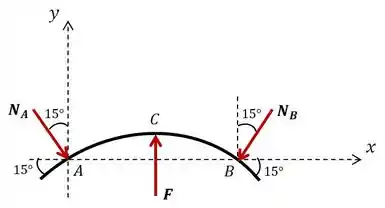
É um problema bem simples! Vamos começar fazendo o somatório da equação de equilíbrio para o eixo :
Com isso temos que as reações em e em são iguais! O que reduz o nosso problema a apenas uma incógnita.
Passo 2
Show, para descobrir o módulo das reações, vamos fazer o somatório da equação de equilíbrio para o eixo :
Como :
Super tranquilo né? Partiu para a próxima!
HYPERLINK "https://emojiterra.com/pt/rosto-piscando/" 