A tesoura para poda mostrada na figura consiste em duas lâminas e dois cabos. Os dois cabos da ferramenta estão ligados pelo pino , e as duas lâminas estão ligadas pelo pino . A lâmina da esquerda e da direita estão ligadas pelo pino ; a lâmina da direita e a da esquerda estão ligadas pelo pino . Determine a intensidade das forças exercidas sobre o pequeno galho quando duas forças de são aplicadas nos cabos da ferramenta como mostra a figura.
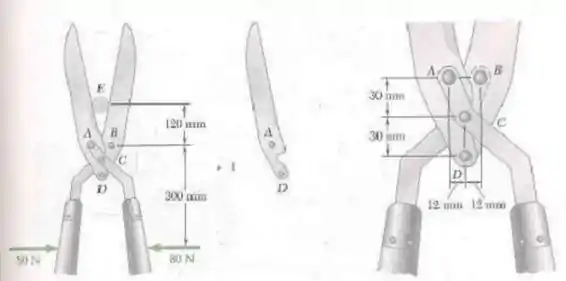
Passo 1
Analisando, primeiramente, a simetria do problema podemos perceber que . Então, considerando que vamos ter . Portanto, todas as forças só possuem componentes horizontais. Agora, para a alça direita teremos
Já para a alça da esquerda teremos