Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 8
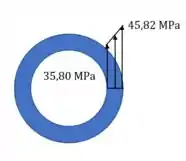
O eixo tem diâmetro externo de e diâmetro interno de . Se for submetido aos torques mostrados na figura, faça o gráfico da distribuição de tensão de cisalhamento que age ao longo de uma linha radial que se encontra no interior da região do eixo. Os mancais lisos em e não resistem a torque.
Passo 1
Vários torques são aplicados em um eixo vazado. Os mancais em que o eixo está apoiado não resistem a torque, então não geram torque!
Queremos descobrir a distribuição tensão de cisalhamento numa seção transversal em !
Sabemos que a fórmula da torção para cisalhamento é
Características do eixo:
- Raio externo: .
- Raio interno: .
- Momento polar de inércia: .
O é constante pro eixo todo. O na fórmula a gente sabe que varia de a . Ah, então primeiro a gente precisa descobrir o valor do torque para essa região que queremos estudar!
Passo 2
Precisamos descobrir qual é o torque.
Primeiro, escolha um sentido do torque pra ser positivo. Vamos escolher o sentido a para isso. Aponte seu dedão direito nesse sentido. Se o torque seguir seus dedos quando fecham, é positivo. Se não seguir, negativo
Aí quebre o eixo em seções. Vamos por partes, calculando o torque. Lembre-se que os mancais não resistem a torção nessa questão!
- Torque na seção até : .
- Torque na seção até o final: .
Ótimo, nossa conta fechou com o do final da figura (equilíbrio!), então está tudo certo.
O torque que queremos, na região , é .
Passo 3
Agora vamos desenhar. A fórmula a tensão varia de acordo com o raio! E linearmente!
O máximo da tensão vai ser
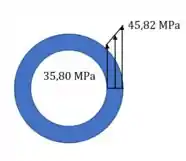
Para calcular aquele valor menor ali na figura, é só usar a fórmula no raio interno.
Resposta
