Um eixo é feito de uma liga de aço com tensão de cisalhamento admissível . Se o diâmetro do eixo for , determine o torque máximo que pode ser transmitido. Qual seria o torque máximo se fosse feito um furo de de diâmetro no eixo? Faça um rascunho da distribuição da tensão de cisalhamento ao longo de uma linha radial em cada caso.
Passo 1
Falaaa! Vamos começar!
Estamos interessados no cisalhamento de um eixo causado por torção.
Sabemos que a fórmula da torção para cisalhamento é
Show, vamos ver quais dessas letras nós conhecemos sobre o eixo.
Características do eixo:
- Raio do eixo: .
- Tensão admissível: .
Queremos descobrir o torque máximo que o eixo com essas propriedades pode suportar.
Depois queremos saber qual seria o torque máximo se fizermos um furo de de diâmetro no eixo!
Passo 2
Para a primeira parte, é só aplicarmos já a fórmula e achar o torque máximo! Como assim? O torque máximo vai gerar a tensão cisalhante máxima admissível, certo?
Então podemos fazer:
Com nesse caso, a nossa seção transversal é maciça de raio , o momento polar de inércia fica
E aí é substituir o que a gente tem na fórmulinha da tensão e:
Passo 3
Ótimo, agora temos que ver qual é o torque máximo quando pensamos esse eixo com um furo de de diâmetro!
Vamos precisar calcular um novo momento polar inércia: . Esse vai ser o original menos o momento polar de inércia do material perdido com esse furo! Vejamos a fórmula:
Como o furo tem de diâmetro, o é . Bora calcular logo o então!
Passo 4
Agora só voltar pra fórmula e achar o !
Passo 5
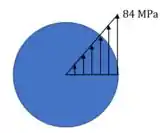
Agora vamos desenhar a distribuição de tensão na seção. O que ele quer aqui é uma representação de como a tensão varia com o raio (por isso que ele fala ao longo de uma linha radial). Como se o fosse o nosso valor de de uma reta.
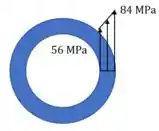
Para o primeiro caso, sem o furo, veja que na fórmula a tensão varia de acordo com o raio somente! E linearmente!
Então a tensão vai ser uma reta do zero até o valor máximo de que ocorre no maior valor de , ou seja, na borda.
Passo 6
Vejamos como fica a distribuição de tensão pra quando temos um furo! Olha pra fórmula:
Ainda depende do raio! O resto das letras na direita são constantes. Então a tensão também vai variar linearmente com o raio. Só que não vamos ter tensão onde não tem material, obviamente.
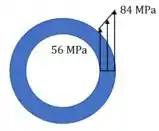
Para calcular aquele valor menor ali na figura, é só usar a fórmula no raio interno.
Resposta
Torque máximo para o eixo maciço: . Distribuição de tensão:
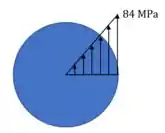
Torque máximo para eixo com furo: . Distribuição de tensão: