Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 125
A unidade de força A do trator-raspador tem uma massa de 4 Mg com centro de massa em G1. A unidade raspadora de reboque totalmente carregada B tem uma massa de 24 Mg com centro de massa em G2. O posicionamento do raspador é controlado por dois cilindros hidráulicos EF, um em cada lado da máquina. Calcule a compressão F em cada um dos cilindros e a magnitude da força suportada por cada um dos pinos em H, um de cada lado. Suponha que as rodas estejam livres para girar, de modo que não haja componentes horizontais de força sob as rodas.
Passo 1
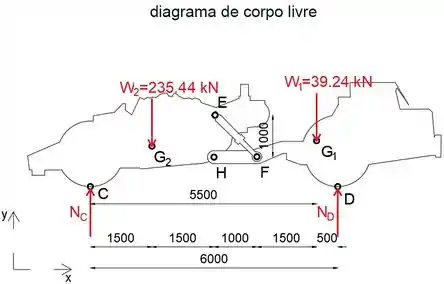
Primeiro, vamos isolar e desenhar o diagrama de corpo livre de todo o raspador para determinar as forças de reação em C e D
O peso da unidade de potência A é:
O peso da unidade B carregada é:
Passo 2
Equacionando a soma dos momentos sobre o ponto C a zero, podemos determinar a força de reação normal em D
Passo 3
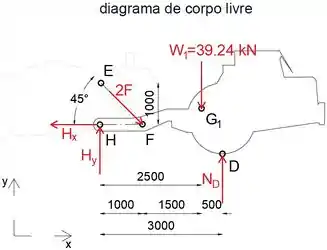
A seguir, vamos isolar e desenhar o diagrama de corpo livre da unidade de energia A
Observe que existem dois cilindros e pinos H no lado do cache
O ângulo que o cilindro EF faz com a horizontal é:
Passo 4
Equacionando a soma dos momentos sobre o ponto H a zero, podemos determinar a força F
Substitua ND por seu valor
Finalmente, a força no cilindro é:
Passo 5
Ao igualar a soma das forças na direção x e y a zero, podemos determinar as forças de reação em H
Substitua F por seu valor
Passo 6
Substitua F e ND por seus valores
Finalmente, usando o teorema de Pitágoras, podemos calcular a magnitude da força atuando no pino H