Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.3 - Ex. 33
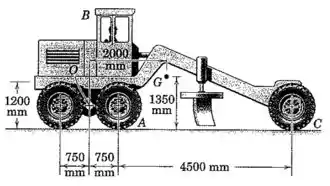
A unidade em série do nivelador de estradas possui uma massa de e é livremente articulada à unidade motriz em , que também é o centro de massa de . A massa da unidade isolada é de , incluindo as rodas , com centro de massa em . Encontre a distância mínima na qual o nivelador é capaz de parar quando se desloca em uma estrada nivelada a (lâmina retraída e motor desengatado) de modo que o par de rodas traseiras da unidade em série não se levante do solo. Os freios estão somente nas rodas em série. Considere cada uma das duas unidades como um corpo rígido.
Passo 1
Nós estamos lidando com dois corpos rígidos separados aqui. O nivelador está encaixado na “unidade motriz” , que é toda a parte de cima do veículo.
Se o sistema inteiro se move com aceleração , então existe uma força resultante agindo em cada parte. Além disso, temos as forças normais, os pesos, e a força de contato no ponto .
Vamos então começar analisando apenas o nivelador no caso limite em que as rodas em estão prestes a perder o contato com o solo, nesse caso não temos forças de contato com o chão:
Então a soma dos momentos em relação ao ponto é:
E isso deve ser igual ao momento da força resultante agindo no centro de massa:
E então ficamos com a seguinte equação:
Passo 2
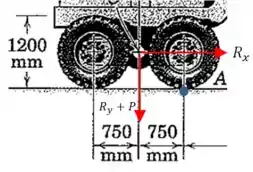
Agora vamos fazer a mesma coisa para a parte de cima do veículo, e dessa vez vamos tomar como referência o contato da roda com o solo no ponto .
Nesse caso, as únicas forças que vão sobrar gerando momento serão:
O peso que age no ponto , a uma distância de :
A força que age no ponto na vertical para cima, a uma distância , e favorece a rotação no sentido oposto ao peso:
A força , apontando na horizontal para a esquerda, a uma distância :
E a soma desses momentos deve ser igual ao momento da força resultante horizontal agindo no centro de massa:
Então ficamos com a seguinte equação:
Passo 3
Então temos o seguinte sistema:
Temos um sistema de três variáveis, e duas equações, então precisamos encontrar mais uma das variáveis antes de resolvê-lo.
Olhando para a parte de cima do veículo, vamos aplicar a segunda lei de Newton na direção horizontal, que é justamente a direção da aceleração .
Apenas a força aponta nessa direção, no mesmo sentido da aceleração :
Substituindo isso no sistema:
Podemos resolver para calcular . Vamos multiplicar a equação de baixo por e somar com a primeira:
Passo 4
Então, se o nivelador está se movendo a , a distância mínima na qual ele é capaz de parar com uma desaceleração de é:
Resposta
A distância mínima é .