Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.4 - Ex. 54
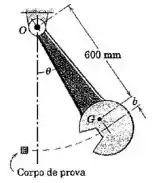
Um dispositivo para ensaio de impacto consiste em um pêndulo de com centro de massa em e raio de giração de em relação a . A distância para o pêndulo é selecionada de modo que a força sobre o mancal em tenha o menor valor possível durante o impacto com o corpo de prova na parte mais baixa da oscilação. Determine e calcule o módulo da força total sobre o mancal logo após a liberação a partir do repouso em .
Passo 1
Para que a força sobre o mancal tenha o menor valor possível, o impacto com o corpo de prova deve ocorrer sobre o ponto de percussão do pêndulo.
Obs.: essa é uma propriedade importante do ponto de percussão: se você bate em uma bola de baseball de forma que ela atinja o ponto de percussão do taco, você não sentirá nenhum impacto na sua mão.
Então é a posição do ponto de percussão em relação ao centro de massa. Podemos usar a fórmula conhecida para calcular a posição em relação ao ponto de suspensão :
Então é:
Passo 2
Agora queremos calcular o módulo da força total sobre o mancal. Outra propriedade útil do ponto de percussão é que a soma dos momentos é sempre nula em relação a ela:
A componente da força peso na direção perpendicular ao pêndulo em é:
E a da componente tangencial da força (que favorece a rotação no sentido oposto) é:
Então:
Passo 3
Agora vamos aplicar a segunda lei de Newton na direção normal para encontrar a componente da força:
E as forças que agem nessa direção são: a outra componente da força peso, e a força que queremos calcular:
E então o módulo da força é:
Resposta
O módulo da força é e .