Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.6 - Ex. 52
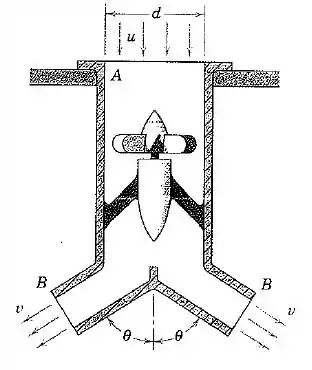
A unidade de ventilação de massa fechada em um duto é apoiada na posição vertical sobre o seu flange em . A unidade aspira ar com uma massa específica e uma velocidade através da seção e o descarrega através da seção com uma velocidade . Ambas as pressões de entrada e de saída são atmosféricas. Escreva uma expressão para a força aplicada ao flange da unidade de ventilação pela laje de suporte.
Passo 1
Nosso objetivo é encontrar a força resultante aplicada sobre a unidade de ventilação. Vamos usar a fórmula para a força resultante em um sistema de escoamento:
Como o sistema está pendurado pelas bordas, a força resultante deve considerar tanto a força que age sobre o ar, quanto a que sustenta o peso da unidade:
Beleza, agora precisamos encontrar os outros termos da equação.
Passo 2
Vamos começar calculando a taxa de escoamento de massa do sistema. Segundo o enunciado, a velocidade com que o ar entra no duto é , então:
E agora vamos ver a variação de velocidades . É importante lembrar que essa é a variação na direção da força, ou seja, precisamos projetar as velocidades no eixo vertical:
E todas ficam com sinal negativo porque apontam para baixo.
Passo 3
E agora substituindo na equação da força resultante:
É só isolar :
Resolvido!
Resposta
A força é dada por .