Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Estatica das Estruturas por Humberto Lima Soriano- Ed: 3º - Capítulo 1.9 - Ex. 4

Urn poste de comprimento l área de seção transversal constante A e material de peso específico ρ deve ser içado por um cabo colocado a 2/3 de sua extremidade inferior, para encaixe em uma base de concreto que faceia o nível do solo, como ilustra a parte esquerda da próxima figura. Determine o valor da força de içamento

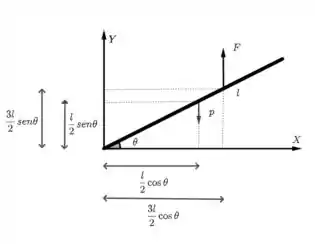
Passo 1

Ao ser içado, o posto será rotacionado em torno do ponto ( x , y ) = ( 0,0 ) , que será o ponto de apoio. Ou seja, não haverá translação horizontal ou vertical, somente rotação. Num dado momento, o poste fará um ângulo θ com o eixo. Teremos a força peso e a força de içamento, e a soma dos momentos dessas duas forças em relação ao ponto de apoio deve ser nula ∑ M → = 0 → .

Primeiramente, vamos reduzir a força peso atuando no poste a origem do sistema. Para isso, vamos considerar o posto ainda no solo, antes do içamento, para facilitar os nossos cálculos. Em geral, a força peso é dada pela massa de uma partícula vezes a aceleração da gravidade g = 9,8   m / s 2 . Como o poste pode ser considerado um corpo rígido,a força da gravidade atua em cada pequena seção do poste. Então, para obter a força em cada pequena seção do poste, ou seja, a força por unidade de comprimento, precisamos multiplicar o peso específico pela área transversal do poste:

p = F o r ç a   p e s o   p o r   u n i d a d e   d e   c o m p r i m e n t o = ρ ⋅ A ⋅ g

Quando temos uma força uniformemente distribuída em uma linha ( força por unidade de comprimento), a força resultante é dada por

R = ∫ 0 l p   d x = ∫ 0 l ρ A g   d x = ρ A g ∫ 0 l   d x = ρ A g x | 0 l = ρ   A g   l   .

Agora, vamos calcular o ponto onde a força resultante deve ser aplicada, de modo a ter o mesmo efeito que a força peso atuando em todo o poste:

x R = ∫ 0 l   p   x d x ∫ 0   l   p   d x .

Como ∫ 0 l   p   x d x = ρ A g ∫ 0 l x d x = ρ A g x 2 2 | 0 l = ρ A g l 2 2 , então x R = ρ A g l 2 2 ρ   A g   l   = l 2 , que corresponde ao centro do poste. Ou seja, podemos considerar que a força peso atuando sobre todo o poste é equivalente a uma força com peso total ρ   A   l atuando no ponto central do poste. Isso vai continuar sendo verdade mesmo depois que o porte seja içado: somente a direção da força peso mudará, mas sua magnitude e o ponto onde ela deve ser aplicada permanecem os mesmos.

Passo 2

Agora, podemos calcular o momento gerado pela força peso. O vetor posição para a força peso sai da origem até o ponto central do poste, ou seja, r P → = l 2 c o s θ   i → + l 2   s e n   θ   j → no nosso sistema de coordenadas. A força peso tem módulo ρ   A g   l , como foi calculado no passo anterior, e aponta na direção - j → , ou seja, p → = - ρ   A g   l   j → . Logo, o momento da força peso tem as seguintes componentes

M P X = Y P   p Z - Z P   p Y = l 2   s e n   θ   ⋅ 0 - 0 ⋅ ( - ρ   A g   l ) = 0

M P Y = Z P   p X - X P   p Z = 0 - l 2 c o s θ ⋅ 0   = 0

M P Z = X   P p Y - Y P   p X = l 2 c o s θ ⋅ ( - ρ   A g   l ) - l 2   s e n   θ ⋅ 0 = - l 2   ρ   A   g 2 c o s θ

⇒   M → P = - l 2   ρ   A   g 2 c o s θ   k →

Passo 3

Agora resta calcular o momento da força de içamento. A força de içamento é F → = F   j → enquanto o vetor posição sai da origem até dois terços do poste, isto é, r F → = 2 l 3 c o s θ   i → + 2 l 3   s e n   θ   j → . Agora, vamos determinar o momento da força de içamento

M F X = Y F   F Z - Z F   F Y = 2 l 3   s e n   θ   ⋅ 0 - 0 ⋅ F = 0

M F Y = Z F   F X - X F   F Z = 0 - 2 l 3 c o s θ   ⋅ 0 = 0

M F Z = X   F F Y - Y F   F X = 2 l 3 c o s θ   ⋅ F - 2 l 3   s e n   θ   ⋅ 0 = 2 l   F 3 c o s θ

⇒ M → F = 2 l   F 3 c o s θ   k →

Passo 4

Ok, descobrimos o momento da força peso e o momento da força de içamento. No passo 1 já discutimos que a soma vetorial dessas duas forças deve ser nula. Então

∑ M → = M → P + M → F =   - l 2   ρ   A   g 2   c o s θ   k → + 2 l   F 3   c o s θ   k → = ( - l 2   ρ   A   g 2 + 2 l   F 3 ) c o s θ   k →   =   0 →

Agora, resolvemos a equação acima para encontrar o módulo da força:

⇒ 2 l   F 3 = l 2   ρ   A   g 2   ⇒ F = 3 2 l l 2   ρ   A   g 2 = 3   l   ρ   A   g 4  

Resposta

F → = 3   l   ρ   A   g 4 k ^

Exercícios de Livros Relacionados

Se a força F = 100 N, determine o ângulo θ( 0 ≤ θ ≤ 90 ° ) , de modo que a força desenvolva um momento em sentido horário em relação ao ponto O de 20 N . m.
Determine a intensidade da força F que deverá ser aplicada na extremidade da alavanca, de modo que essa força crie um momento em sentido horário de 15 N . m em relação ao ponto O quando θ = 30 ° .
Determine a intensidade e o sentido direcional da força em A em relação ao ponto P .
A grua pode ser ajustada para qualquer ângulo 0 ° ≤ θ ≤ 90 ° e qualquer extensão 0 ≤ x ≤ 5m . Para uma massa suspensa de 120k g , determine o momento desenvolvido em A em função de x e θ . Que valores
O cabo de reboque exerce uma força P = 6k N na extremidade da lança do guindaste de 8m de comprimento. Se x = 10m , determine a posição θ da lança para que essa força crie um momento máximo em relação