Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 10
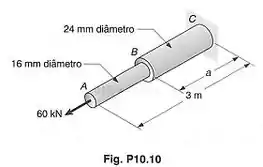
Usando , determinar:
- a energia de deformação da barra de alumínio , quando ;
- a correspondente densidade de energia de deformação nas porções e da barra.
Passo 1
Faaaala, meus queridos! Prontos para uma questão de energia de deformação?
Primeiro, o enunciado quer que a gente calcule a energia de deformação de uma barra sob carga . A barra é formada por duas barras: (mais grossa) e (mais fina). A barra mais grossa possui área de seção transversal constante igual a e diâmetro . A barra mais fina possui área de seção transversal constante igual a e diâmetro .
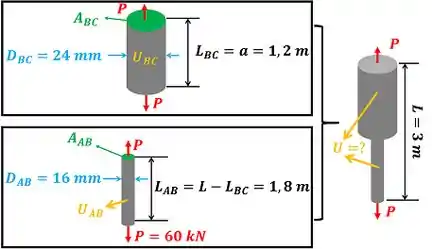
e são as energias de deformação das barras e respectivamente. e são os comprimentos das barras e respectivamente.
Como podemos ver na figura acima, a barra é a soma das barras e . Por causa disso, a energia de deformação da barra total tem que ser igual à soma entre a energia de deformação da barra mais grossa e a energia de deformação da barra mais fina.
A fórmula que calcula as energias de deformação de barras com áreas da seção transversal constantes é a fórmula 10.14 do livro.
Usaremos essa fórmula para e .
onde é o módulo de elasticidade que vale segundo o enunciado.
Sabendo quanto e valem, podemos calcular a segunda informação que o enunciado quer. Ele quer as densidades de energia de deformação nas barras e .
e são as energias de deformação e divididas pelos volumes das barras!
onde é o volume da barra e é o volume da barra .
Agora que temos todas essas informações em mãos, vamos calcular a energia de deformação da barra toda no próximo passo!
Passo 2
Nesse passo nós vamos resolver a letra (a) da questão. Ou seja, calcular a energia de deformação da barra completa. Para isso, calcularemos e .
Antes de calcular esses dois valores, precisamos achar as áreas e em .
Além disso, temos que converter a força de para , multiplicando por .
Por fim, temos que converter de para , multiplicando por .
é a soma desses dois valores! Logo:
Passo 3
Nesse passo nós vamos resolver a letra (b) da questão, calculando e .
Para calcular esses valores, precisamos calcular os volumes das barras e . Eles são obtidos, multiplicando as áreas e por e .
Substituindo os volumes das fórmulas de e , achamos:
Ebaaaaa! Concluímos mais uma questão!!!