Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas - Ex. 126

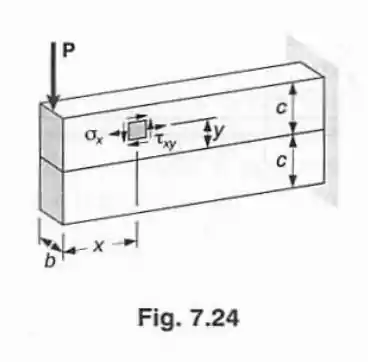
Usando as Eqs. (7,16) e (7,17), mostrar que em qualquer seção transversal da viga da Fig 7.24: (a) as direções dos eixos principais de tensão são definidos pela relação

t g 2 θ 2 p = c 2 - y 2 x y

(b) o máximo valor da tensão normal é:

σ m á x = 3 2 P A x y c 2   1 + 1 + c 2 - y 2 x y 2  

Passo 1

Bom para começar essa questão vamos relembrar as equações que foram mencionadas!

Equação (7.16)

σ x = 3 P A x y c 2

Equação (7.17)

τ x y = 3 2 P A 1 - y 2 c 2

Show de bola! Agora a gente tem que pegar essas equações e mexer nelas até encontrar os termos referentes à direção principal 2 θ p e à tensão normal máxima σ m á x .

Vamos fazer isso pela própria definição desses termos, então vamos lá!

Passo 2

Vamos começar pela equação do ângulo 2 θ p :

t g 2 θ p = 2 τ x y σ x - σ y

Como

σ y = 0

A gente tem que:

t g 2 θ p = 2 τ x y σ x

Agora é só substituir pelas duas equações dadas:

σ x = 3 P A x y c 2

τ x y = 3 2 P A 1 - y 2 c 2

Fica dessa forma:

t g 2 θ p = 2 × 3 2 P A 1 - y 2 c 2 3 P A x y c 2

t g 2 θ p = 1 - y 2 c 2 x y c 2

t g 2 θ p = c 2 - y 2 x y

Passo 3

Agora vamos fazer parecido mas para σ m á x :

σ m á x = σ m é d + R

Como:

σ m é d = σ x + σ y 2

Novamente, σ y = 0

σ m é d = σ x + 0 2 = σ x 2

Substitundo:

σ x = 3 P A x y c 2

Temos

σ m é d = 3 P A x y c 2 2 = 3 2 P A x y c 2

Passo 4

Vamos achar também o raio:

R = σ x - σ y 2 2 + τ x y 2

Novamente, σ y = 0

R = σ x 2 2 + τ x y 2

Substituindo

R = 3 P A x y c 2 2 2 + 3 2 P A 1 - y 2 c 2 2

R = 9 4   P A x y c 2 2 + 9 4 P A   1 - y 2 c 2 2

R = 3 2 P A   x y c 2 2 + 1 - y 2 c 2 2

R = 3 2 P A   x y c 2 2 + 1 - 2 y 2 c 2 + y 4 c 2

Agora vamos colocar o termo x 2 y 2 / c 2 em evidencia dentro da raiz:

R = 3 2 P A   x 2 y 2 c 2 1 + c 2 x y - 2 y x + y 3 x

R = 3 2 P A x y c   1 + c 2 x y - 2 y x + y 3 x

R = 3 2 P A x y c   1 + c 2 x y - 2 y 2 x y + y 4 x y

R = 3 2 P A x y c   1 + c 2 - 2 y 2 + y 4 x y

R = 3 2 P A x y c   1 + c 2 - y 2 x y 2

Passo 5

Agora é só substituir:

σ m á x = σ m é d + R

σ m é d = 3 2 P A x y c 2

R = 3 2 P A x y c   1 + c 2 - y 2 x y 2

Ficamos com:

σ m á x = 3 2 P A x y c 2 + 3 2 P A x y c   1 + c 2 - y 2 x y 2

σ m á x = 3 2 P A x y c 2 1 +   1 + c 2 - y 2 x y 2

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma força vertical de 4kN é aplicada no ponto A de um componente de maquina mostrado. Determinar as tensões principais e a máxima tensão de cisalhamento no:Ponto HPonto K
Várias forças são aplicadas à montagem tubular indicada. Sabendo-se que os diâmetros, interno e externo, do tubo são iguais a 38 m me45 m m , respectivamente, determinar:Os planos e as tensões princip
Uma força vertical de 18k N é aplicada na extremidade A da barra AB, que é soldado a um tubo de alumínio extrudado de espessura uniforme de 6mm. Determinar as tensões principais e a máxima tensão de c
Resolver os P r o b s . 6 . 8 e 6.1 2 , usando o círculo de mohr.
Resolver os P r o b s . 6 . 7 e 6.1 1 , usando o círculo de mohr.