Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas - Ex. 130
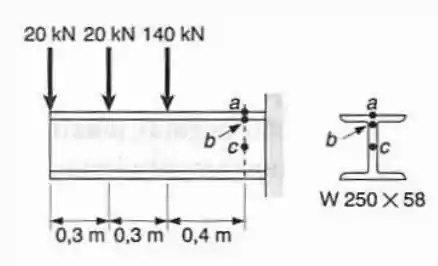
Para a viga e o carregamento mostrado, determinar a máxima tensão normal nos pontos e .
Passo 1
Vamos resolver o problema seguindo o passo a passo:
- Calcular o momento fletor na região
- Calcular a tensão normal para cada ponto, por meio da seguinte equação:
obs: Os valores e são todos dados na tabela!
Passo 2
Para achar o momento fletor basta fazer o somatório do momento igual a zero:
Passo 3
Agora vamos utilizar a nossa equação:
Olhando na tabela vemos que para o perfil :
Substituindo na equação:
Passo 4
Agora para :
é a distância da linha neutra até o ponto que queremos.
é a maior distância desde a linha neutra, ou seja:
Passo 5
Como encontra-se exatamente sobre a linha neutra temos que:
Logo,
Resposta
a)
b)
c)
Exercícios de Livros Relacionados
No eixo de um automóvel atuam as forças e o torque mostrado. Sabendo-se que o diâmetro do eixo é de 30mm, determinar: (a) os planos principais e as tensões principais no ponto H, localizado no cume da
As fibras de uma peça de madeira formam um ângulo de 18 graus com a vertical. Para o estado de tensões mostrado determinar: (a) a tensão de cisalhamento no plano, em um plano paralelo as fibras;(b) a
Para o estado de tensões dado, determinar as tensões, normal e de cisalhamento, depois que o elemento mostrado tenha sofrido uma rotação de:(b) 15 no sentido horário
Uma força de 19,5kN é aplicada no ponto D da barra de ferro fundido mostrada. Saendo-se que a barra tem um diâmetro de 60mm, determinar as tensões principais e a máxima tensão de cisalhamento no:(a) p
Para o estado de tensões dado, determinar as tensões, normal e de cisalhamento, depois que o elemento mostrado tenha sofrido uma rotação de:(a) 40 no sentido anti-horário