Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 57
Um colar de desloca-se ao longo da barra uniforme e choca-se com uma pequena placa presa na extremidade da barra, com uma velocidade . Usando e sabendo-se que a tensão admissível na barra é de , determinar o maior diâmetro que pode ser usado para a barra.
Passo 1
Fala aí, pessoas lindas! Como vai a vida?
Vamos fazer um exercício de carregamento axial produzido por impacto?
Essa questão quer saber qual é o valor de diâmetro da barra que faz a tensão máxima na produzida pelo impacto ser igual à tensão admissível .
Ou seja, o colar de massa com velocidade se choca com a ponta da barra, produzindo uma tensão máxima nela e queremos saber o diâmetro que faz essa tensão valer . A tensão máxima axial produzida em uma barra de comprimento e módulo de elasticidade e volume é calculada através da equação 10.39 do livro.
A figura abaixo mostra os dados que temos para calcular .
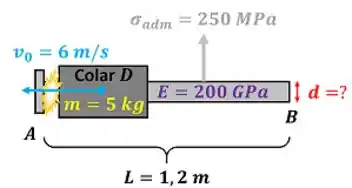
Agora que entendemos o que precisamos calcular, vamos começar a resolver o exercício no próximo passo.
Passo 2
Nós que queremos calcular o diâmetro da barra, mas até agora nós só vimos fórmulas onde o diâmetro da barra não aparece. Para fazer o aparecer, temos que lembrar que o volume da barra cilíndrica vale:
Substituindo isso na equação de , achamos:
Substituindo na equação de e reorganizando a equação, somos capazes de criar uma fórmula para calcular .
Passo 3
Nós já temos tudo o que precisamos para achar ! Mas vamos com calma! Antes de substituir os valores que temos na equação de , precisamos converter as unidades de e .
Temos que passar de para , multiplicando o valor por e temos que converter de para , multiplicando por .
Agora sim podemos calcular !
Obaaaaa! Já acabamos com o exercício!