Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 4.Problemas - Ex. 179
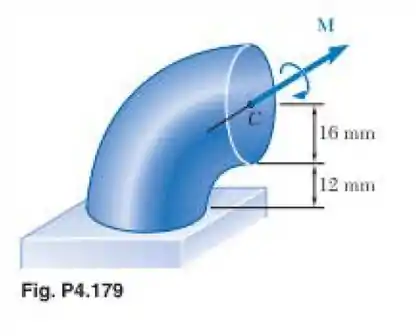
A barra curva mostrada tem seção circular com 32 mm de diâmetro. Determine o maior momento M em relação ao eixo horizontal que pode ser aplicado na barra se a tensão máxima não exceder 60 MPa.
Passo 1
Beleza! Vamos começar esse exercício escrevendo o raio interno da seção, que pode ser visto através da figura do enunciado, então temos:
Agora, para o raio externo da seção, que será dado pelo raio interno mais o diâmetro da seção, teremos:
Agora vamos escrever o raio médio da seção, que será dado por:
Agora vamos calcular a área da seção, então temos:
Agora, para encontrar a localização do raio da superfície neutra da seção, vamos recorrer a fórmula para o círculo apresentada na figura 4.61 dessa seção, onde temos:
Em que é o raio da seção. Então substituindo os valores conhecidos nessa equação, temos:
Passo 2
Agora podemos encontrar a excentricidade da seção, que é a distância entre a linha neutra e o centroide da seção, através de:
Substituindo os valores conhecidos, teremos:
Passo 3
Agora, para encontrar o maior momento M em relação ao eixo horizontal que pode ser aplicado na barra , vamos utilizar a equação 4.71 vista nessa seção, dada por:
Isolando o momento dessa equação, chegamos em:
Vamos calcular o momento para dois pontos da seção, a extremidade inferior, em , que chamaremos de ponto A, e em que chamaremos de ponto B. Começando pelo ponto A, teremos:
Agora, repetindo o cálculo anterior, só que para o ponto B, teremos:
Então, o máximo valor admissível deve ser o menor valor (em módulo) dos dois momentos encontrados, dessa forma, teremos: