Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas - Ex. 46
Usando o método da Sec. 7.4, resolver o Prob. 7.18
Passo 1
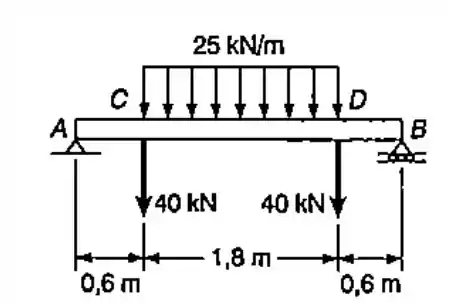
Pessoal essa questão pede para fazermos o diagrama do momento fletor e da força cortante para a viga representada. A primeira coisa que temos de fazer é achar as forças de reação em e em .
Para este exercício iremos calcular a força cortante aplicando diversos cortes na seção e finalmente vamos calcular o momento fletor por meio da integral da cortante:
Passo 2
Vamos começar calculando as reações:
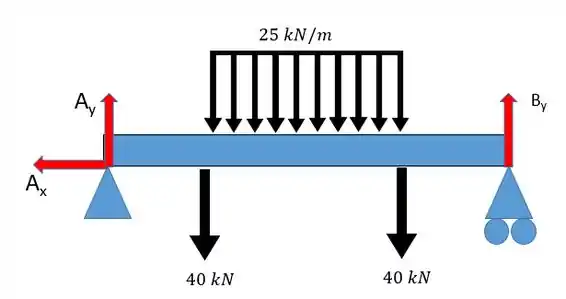
Como só existe uma força em essa força é nula, portanto . Agora podemos aplicar as equações da estática:
Repare que o termo é o valor da força relacionada à carga distribuída e é calculada como:
Voltando à equação:
Como o carregamento é simétrico então vamos ter que as reações são iguas:
Passo 3
Agora vamos calcular a força cortante na seção :
Perceba que a cortante deve ser igual à força de reação em , logo:
Para o trecho :
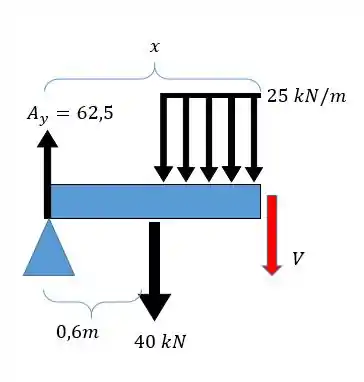
Aqui o valor da cortante vai ter que ser:
O termo representa a carga de vezes o comprimento que essa carga atua , assim vamos ter:
Galera como o problema é simétrico então o trecho será igual ao trecho só que negativo:
Desenhando o diagrama:
Podemos ver que a força cortante máxima se localiza nas extremidades e vale:
Passo 4
Agora para calcular o momento fletor é só integrar a equação da força cortante:
Para o trecho :
Aí a gente vê quanto vale no ponto :
Para o trecho :
Sendo o momento da força de assim vamos ter:
Calculando para o centro da viga (que, pelo fato da viga ser simétrica é ponto de máximo momento fletor):
Depois é só aplicar a simetria e temos a outra metade da viga, fazendo o diagrama:
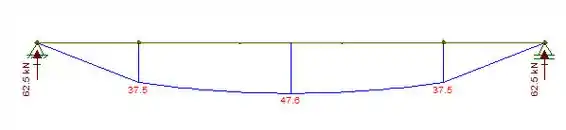
Resposta
a)
b)