Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 80

Usando o método do trabalho e energia, determinar a deflexão no ponto , devido à carga .

Passo 1

Oi, pessoal! Tudo bem? Vamos resolver um exercício de deflexão através do método de energia?

Essa questão mostra uma viga sendo carregada com uma força . Essa força faz a barra absorver uma energia e se deformar. O enunciado pede que a gente ache a deflexão no ponto da viga, usando duas equações de . A primeira, calcula a partir da força .

A segunda, calcula por meio de uma integral do momento fletor da viga.

Igualando essas duas equações de , achamos .

A figura abaixo mostra os dados que temos para achar .

é a força de reação causada pela restrição no ponto e é a força de reação causada pela restrição no ponto . Precisamos apenas uma das forças para encontrar o momento . No próximo passo, calcularemos .

Passo 2

A primeira etapa para fazer isso é encontrar a reação fazendo o equilíbrio de momentos em relação ao ponto .

Como a força faz a barra tender a girar no sentido horário, vamos colocar um sinal de menos na frente do momento de .

Agora estamos aptos a achar ! Para achar precisamos usar a equação de equilíbrio de momento na parte direita da barra . Calcularemos o equilíbrio no ponto . O momento tem dois valores: um quando a parte direita da barra ainda não inclui a força e outro quando a parte direita inclui a força . Vamos começar o cálculo do primeiro valor de .

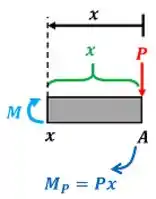
Colocamos um sinal de menos na frente dos momentos e , porque os dois fazem a viga girar no sentido horário.

Agora vamos calcular o segundo valor de .

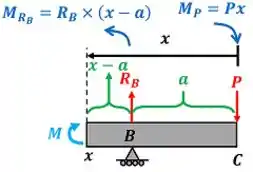
Com esses valores de , podemos achar a partir da integral para encontar !

Passo 3

tem dois valores. Um quando vale entre e e outro, quando vale entre e .

Por isso, para substituir na integral que calcula , precisamos separar a integral em duas. Uma que vai de a para o primeiro valor de e outra que vai de a para o segundo valor de .